题目内容
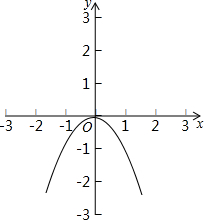 (2007•海淀区一模)已知,如图,在平面直角坐标系xOy中,抛物线l1的解析式为y=-x2,将抛物线l1平移后得到抛物线l2,若抛物线l2经过点(0,2),且其顶点A的横坐标为最小正整数.
(2007•海淀区一模)已知,如图,在平面直角坐标系xOy中,抛物线l1的解析式为y=-x2,将抛物线l1平移后得到抛物线l2,若抛物线l2经过点(0,2),且其顶点A的横坐标为最小正整数.(1)求抛物线l2的解析式;
(2)说明将抛物线l1如何平移得到抛物线l2;
(3)若将抛物线l2沿其对称轴继续上下平移,得到抛物线l3,设抛物线l3的顶点为B,直线OB与抛物线l3的另一个交点为C.当OB=OC时,求点C的坐标.
分析:(1)根据抛物线l2经过点(0,2),即可求出c的值,再利用其顶点A的横坐标为最小正整数,求出b的值即可;
(2)根据配方法得出y=-x2+2x+2=-(x-1)2+3,即可得出图象的平移方向;
(3)利用OB=OC,且B、O、C三点在同一条直线上,点B与点C关于原点对称,进而得出点C的坐标为(-1,-m)代入抛物线l3的解析式y=-(x-1)2+m,求出即可.
(2)根据配方法得出y=-x2+2x+2=-(x-1)2+3,即可得出图象的平移方向;
(3)利用OB=OC,且B、O、C三点在同一条直线上,点B与点C关于原点对称,进而得出点C的坐标为(-1,-m)代入抛物线l3的解析式y=-(x-1)2+m,求出即可.
解答:解:(1)设抛物线l2的解析式为y=-x2+bx+c.
∵点(0,2)在抛物线l2上,
∴y=-x2+bx+2.
∵抛物线l2的顶点的横坐标为1,
∴b=2.
∴l2的解析式为y=-x2+2x+2.
(2)∵y=-x2+2x+2=-(x-1)2+3,
∴将抛物线l1:y=-x2的图象向右平移1个单位长度,再向上平移3个单位长度,可以得到抛物线l2.(答案不唯一)
(3)设顶点B的坐标为(1,m),
则抛物线l3的解析式为y=-(x-1)2+m.
∵OB=OC,且B、O、C三点在同一条直线上,
∴点B与点C关于原点对称.
∴点C的坐标为(-1,-m).
∵点C在抛物线l3上,
∴-m=-(-1-1)2+m.
∴m=2.
∴点C的坐标为(-1,-2).
∵点(0,2)在抛物线l2上,
∴y=-x2+bx+2.
∵抛物线l2的顶点的横坐标为1,
∴b=2.
∴l2的解析式为y=-x2+2x+2.
(2)∵y=-x2+2x+2=-(x-1)2+3,
∴将抛物线l1:y=-x2的图象向右平移1个单位长度,再向上平移3个单位长度,可以得到抛物线l2.(答案不唯一)
(3)设顶点B的坐标为(1,m),
则抛物线l3的解析式为y=-(x-1)2+m.
∵OB=OC,且B、O、C三点在同一条直线上,
∴点B与点C关于原点对称.
∴点C的坐标为(-1,-m).
∵点C在抛物线l3上,
∴-m=-(-1-1)2+m.
∴m=2.
∴点C的坐标为(-1,-2).
点评:此题主要考查了二次函数的综合应用以及图象的平移和点的坐标性质,根据已知得出点B与点C关于原点对称,点C的坐标为(-1,-m)是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 (2007•海淀区一模)科技馆为某机器人编制一段程序,如果机器人在平地上按照图中的步骤行走,那么该机器人所走的总路程为( )
(2007•海淀区一模)科技馆为某机器人编制一段程序,如果机器人在平地上按照图中的步骤行走,那么该机器人所走的总路程为( )