题目内容
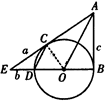
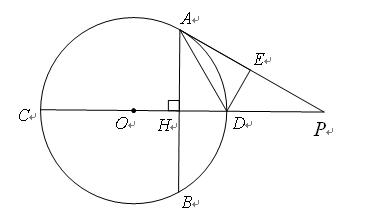
(本题满分9分)如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O
上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.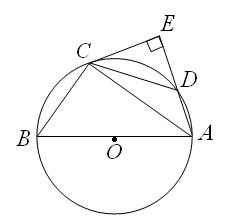
上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.

(1)证明:连接OC······································································· 1分

∵OA=OC
∴∠OAC=∠OCA
∵CE是⊙O的切线
∴∠OCE=90° ·············································· 2分
∵AE⊥CE
∴∠AEC=∠OCE=90°
∴OC∥AE ·················································· 3分
∴∠OCA=∠CAD ∴∠CAD=∠BAC
∴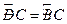
∴DC=BC ··························································································· 4分
(2)∵AB是⊙O的直径 ∴∠ACB=90°
∴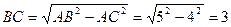 ·························································· 5分
·························································· 5分
∵∠CAE=∠BAC ∠AEC=∠ACB=90°
∴△ACE∽△AB C······················································································ 6分
C······················································································ 6分
∴ ∴
∴
 ······················································ 7分
······················································ 7分
∵DC=BC=3
∴ ····················································· 8分
····················································· 8分
∴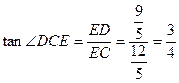 -----------9分 (其它解法参考得分)
-----------9分 (其它解法参考得分)

∵OA=OC
∴∠OAC=∠OCA

∵CE是⊙O的切线
∴∠OCE=90° ·············································· 2分
∵AE⊥CE
∴∠AEC=∠OCE=90°
∴OC∥AE ·················································· 3分
∴∠OCA=∠CAD ∴∠CAD=∠BAC
∴
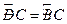
∴DC=BC ··························································································· 4分
(2)∵AB是⊙O的直径 ∴∠ACB=90°
∴
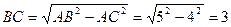 ·························································· 5分
·························································· 5分∵∠CAE=∠BAC ∠AEC=∠ACB=90°
∴△ACE∽△AB
 C······················································································ 6分
C······················································································ 6分∴
 ∴
∴
 ······················································ 7分
······················································ 7分∵DC=BC=3
∴
 ····················································· 8分
····················································· 8分∴
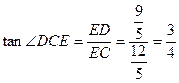 -----------9分 (其它解法参考得分)
-----------9分 (其它解法参考得分)略

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 ,圆周角
,圆周角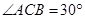 ,则⊙O的直径等于 _________________
,则⊙O的直径等于 _________________ .
.

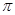 ).
).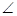 PAB=
PAB=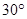 ,
,
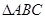 中,
中,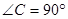 ,且两边长分别为4
,且两边长分别为4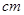 和5
和5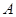 为圆心,3
为圆心,3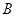 为圆心,2
为圆心,2