题目内容
已知两圆相交,其圆心距为6,大圆半径为8,则小圆半径r的取值范围是( )
(A)r>2 (13)2<r<14 (C)l<r<8 (13)2<r<8
(A)r>2 (13)2<r<14 (C)l<r<8 (13)2<r<8
D
根据两圆相交,则小圆半径r的取值范围是8-r<6<8+r.
解答:解:∵两圆相交,
∴小圆半径r的取值范围是8-r<6<8+r,即2<r,
而r<8,
∴2<r<8
故选D.
点评:本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法.两圆的半径分别为R和r,且R≥r,圆心距为P,则外离:P>R+r;外切:P=R+r;相交:R-r<P<R+r;内切;P=R-r;内含:P<R-r.
解答:解:∵两圆相交,
∴小圆半径r的取值范围是8-r<6<8+r,即2<r,
而r<8,
∴2<r<8
故选D.
点评:本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法.两圆的半径分别为R和r,且R≥r,圆心距为P,则外离:P>R+r;外切:P=R+r;相交:R-r<P<R+r;内切;P=R-r;内含:P<R-r.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目

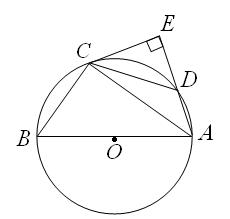
 (1)求证: ;
(1)求证: ;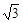 cm
cm 中,
中, ,
, ,点
,点 从
从 开始沿折线A-B-C-D以4cm/s的速度移动,点
开始沿折线A-B-C-D以4cm/s的速度移动,点 从
从 开始沿
开始沿 边以1cm/s的速度移动,如果点
边以1cm/s的速度移动,如果点 时,另一点也随之停止运动。设运动时间为t(s)。
时,另一点也随之停止运动。设运动时间为t(s)。 为矩形?
为矩形? 和
和 的半径都是2cm,那么t为何值时,
的半径都是2cm,那么t为何值时,
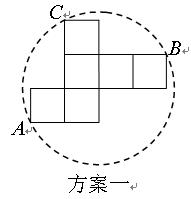
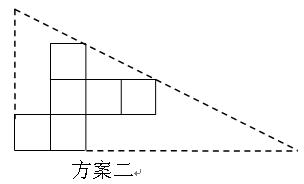

 纸片利用率=
纸片利用率= ×100%
×100% 你认为小明的这个发现是否正确,请说明理由.
你认为小明的这个发现是否正确,请说明理由.
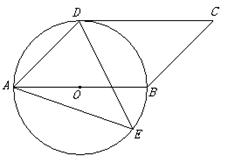
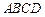 是平行四边形,以AB为直径的⊙O经过点D,点E是⊙O上一点,且∠AED=45°。
是平行四边形,以AB为直径的⊙O经过点D,点E是⊙O上一点,且∠AED=45°。 ,
, ,求∠ADE的正弦值.
,求∠ADE的正弦值.