题目内容
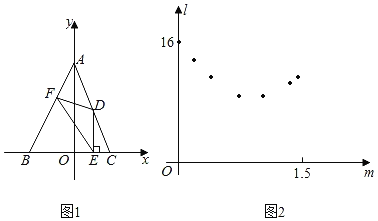
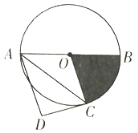
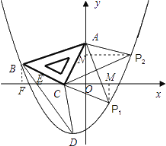
【题目】如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(1,0),点B在抛物线y=ax2+ax2上.
(1)点A的坐标为 ,点B的坐标为 ;抛物线的解析式为 ;
(2)设抛物线的顶点为D,求△DBC的面积;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
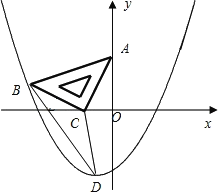
【答案】(1)A(0,2);B(![]() ,1);
,1);![]() (2)
(2)![]() (3)P(
(3)P(![]() ,
,![]() )或(2,1)
)或(2,1)
【解析】
(1)过点B作BF⊥x轴于F,先根据勾股定理求出OA的长,即可得出点A的坐标,再求出OF、BF的长即可求出B的坐标;再把点B的坐标代入抛物线的解析式,求出a的值,即可求出抛物线的解析式;
(2)先求出点D的坐标,再用待定系数法求出直线BD的解析式,设直线BD与x轴交点为E,求出CE的长,再根据S△DBC=S△CEB+S△CED进行计算即可;
(3)假设存在点P,①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,过点P1作P1M⊥x轴,由全等三角形的判定定理可得△MP1C≌△FBC,再由全等三角形的对应边相等可得出点P1点的坐标;
②若以点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,由全等三角形的性质可得出点P2的坐标;点P1、P2的坐标代入抛物线的解析式进行检验即可.
(1)∵C(-1,0),AC=![]() ,
,
∴OA=![]() =2,
=2,
∴A(0,2);
过点B作BF⊥x轴于F,垂足为F,
∵∠ACO+∠CAO=90,∠ACO+∠BCF=90,
∴∠CAO=∠BCF,
在ΔAOC和ΔCFB中,
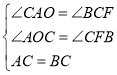 ,
,
∴ΔAOC≌ΔCFB,
∴CF=AO=2,BF=CO=1,
∴OF=3,
∴B(-3,1);
把B(-3,1)代入y=ax2+ax2中,得:1=9a-3a-2,
解得:a=![]() ,
,
∴抛物线的解析式为y=![]() x2+
x2+![]() x2,
x2,
故答案为:A(0,2);B(![]() ,1);
,1);![]() ;
;
(2)由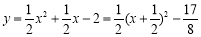 知,抛物线的顶点坐标D(
知,抛物线的顶点坐标D(![]() ,
,![]() ),
),
设直线BD的关系式为y=kx+b,将点B、D的坐标代入得:
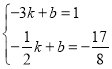 ,
,
解得: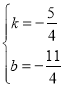 ,
,
∴直线BD的解析式为![]() ,设直线BD与x轴交于点E,
,设直线BD与x轴交于点E,
则点E(![]() ,0),CE=
,0),CE=![]() ,
,
∴S△DBC=S△CEB+S△CED=![]() =
=![]() ;
;
(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;
则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,
过点P1作P1M⊥x轴,
∵CP1=BC,∠MCP1=∠BCF,∠P1MC=∠BFC=90 °,
∴△MP1C≌△FBC.
∴CM=CF=2,P1M=BF=1,
∴P1(1,-1);
②若以点A为直角顶点;
则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,
过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,
∴NP2=OA=2,AN=OC=1,
∴P2(2,1),
经检验,点P1(1,-1)与点P2(2,1)都在抛物线![]() 上.
上.
综上所述,满足条件的P坐标为(![]() ,
,![]() )或(2,1).
)或(2,1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案