题目内容
【题目】(1)问题发现
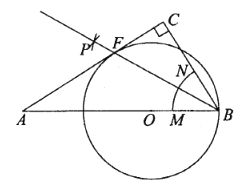
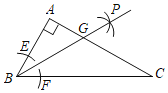
如图1,![]() ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
ABC是等边三角形,点D,E分别在边BC,AC上,若∠ADE=60°,则AB,CE,BD,DC之间的数量关系是 .
(2)拓展探究
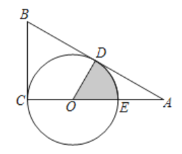
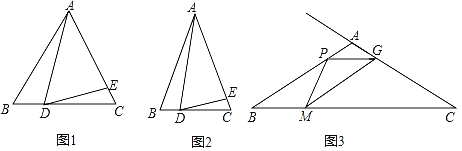
如图2,![]() ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
ABC是等腰三角形,AB=AC,∠B=α,点D,E分别在边BC,AC上.若∠ADE=α,则(1)中的结论是否仍然成立?请说明理由.
(3)解决问题
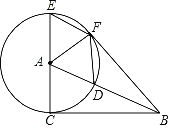
如图3,在![]() ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以
ABC中,∠B=30°,AB=AC=4cm,点P从点A出发,以1cm/s的速度沿A→B方向勾速运动,同时点M从点B出发,以![]() cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
cm/s的速度沿B→C方向匀速运动,当其中一个点运动至终点时,另一个点随之停止运动,连接PM,在PM右侧作∠PMG=30°,该角的另一边交射线CA于点G,连接PC.设运动时间为t(s),当△APG为等腰三角形时,直接写出t的值.
【答案】(1)![]() ;(2)结论成立,见解析;(3)1或2
;(2)结论成立,见解析;(3)1或2
【解析】
(1)问题发现:通过角的关系可证△ABD∽△DCE,根据相似三角形对应边成比例可得到线段的关系;
(2)拓展探究:可证明△ABD∽△DCE,即可得到结论;
(3)解决问题:可证△PBM∽△MCG,然后得到![]() ,用t可表示线段的长,当G点在线段AC上时,若△APG为等腰三角形时,则AP=AG,代入计算即可;当G点在CA延长线上时,若△APG为等腰三角形时,则△APG为等边三角形,代入计算得到t.
,用t可表示线段的长,当G点在线段AC上时,若△APG为等腰三角形时,则AP=AG,代入计算即可;当G点在CA延长线上时,若△APG为等腰三角形时,则△APG为等边三角形,代入计算得到t.
解:(1)问题发现
AB,CE,BD,DC之间的数量关系是:![]() ,
,
理由:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAD+∠ADB=180°﹣60°=120°,∠ADE=60°,
∴∠CDE+∠ADB=180°﹣60°=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴![]() .
.
故答案为:![]() .
.
(2)拓展探究
(1)中的结论成立,
∵AB=AC,∠B=α,
∴∠B=∠C=α,
∴∠BAD+∠ADB=180°﹣α,
∵∠ADE=α,
∴∠CDE+∠ADB=180°﹣α,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴![]() ;
;
(3)解决问题
∵∠B=30°,AB=AC=4cm,
∴∠B=∠C=30°,
∴∠BPM+∠PMB=180°﹣30°=150°,
∵∠PMG=30°,
∴∠CMG+∠PMB=180°﹣30°=150°,
∴∠BPM=∠CMG,
又∠B=∠C=30°,
∴△PBM∽△MCG,
∴![]() ,
,
由题意可知AP=t,BM=![]() t,即BP=4﹣t,
t,即BP=4﹣t,
如图1,过点A作AH⊥BC于H,
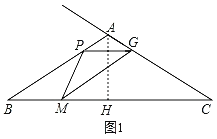
∵∠B=30°,AB=AC=4cm,
∴AH=2cm,BH=![]() =
=![]() =2
=2![]() cm,
cm,
∵AB=AC,AH⊥BC,
∴BC=2BH=4![]() cm,
cm,
∴MC=(4![]() t)cm,
t)cm,
∴![]() ,即CG=3t,
,即CG=3t,
当G点在线段AC上时,若△APG为等腰三角形时,则AP=AG,如图2,

此时AG=AC﹣CG=4﹣3t,
∴4﹣3t=t,
解得:t=1,
当G点在CA延长线上时,若△APG为等腰三角形时,如图3,
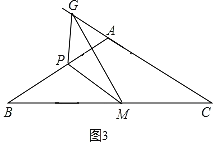
此时∠PAG=180°﹣120°=60°,则△APG为等边三角形,AP=AG,
此时AG=CG﹣AC=3t﹣4,
∴3t﹣4=t,
解得:t=2,
∴当△APG为等腰三角形时,t的值为1或2.

 名校课堂系列答案
名校课堂系列答案