��Ŀ����
����Ŀ���α�����һ�����⣺
��һ��������״��ͼ1���ϲ���һ����Բ���²���һ�����Σ������������IJ����ܳ�Ϊ6m�����������������ʹ��������
�������Ĵ��ǣ���������Բ�İ뾶ԼΪ0.35mʱ����������ֵԼΪ1.05m2��
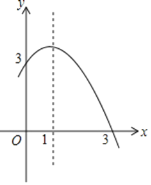
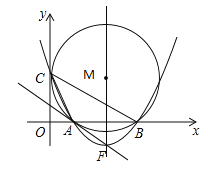
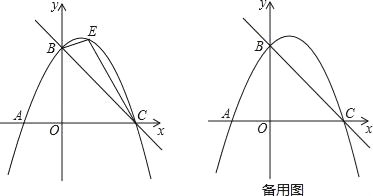
��������ı������������״���ϲ���Ϊ��������������ɵľ��Σ���ͼ2�������ܳ���Ϊ6m������ͼ3������������⣺

��1����ABΪ1m�����ʱ�������������
��2����α��е�����Ƚϣ��ı䴰����״��������������ֵ��û�б����ͨ������˵����
���𰸡���1��![]() ����2�����ֵΪ
����2�����ֵΪ![]() ����������������ֵ�����.
����������������ֵ�����.
��������
��1�����ݾ��κ������ε��ܳ����н�ɣ�
��2����ABΪxcm�����ö��κ�������ֵ��ɣ�
��1������֪�ɵã�AD=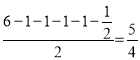 ��S=1��
��S=1��![]() m2��
m2��
��2����AB=xm����AD=3��![]() xm�� ��3-
xm�� ��3-![]() x
x![]() 0 ��
0 ��![]() ��
��
�贰�����ΪS������֪�ã�S=AB��AD=x��3-![]() x��=
x��=![]()
��x=![]() mʱ����x=
mʱ����x=![]() m��
m��![]() �ķ�Χ�ڣ�S���ֵ=
�ķ�Χ�ڣ�S���ֵ=![]() ��
��
����α��е�����Ƚϣ����ڴ�������������ֵ���

��ϰ��ϵ�д�
�����Ŀ