题目内容
【题目】如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( )
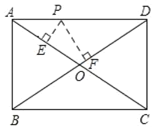
A.6B.12C.24D.不能确定
【答案】B
【解析】
由矩形ABCD可得:S△AOD=![]() S矩形ABCD,又由AB=15,BC=20,可求得AC的长,则可求得OA与OD的长,又由S△AOD=S△APO+S△DPO=
S矩形ABCD,又由AB=15,BC=20,可求得AC的长,则可求得OA与OD的长,又由S△AOD=S△APO+S△DPO=![]() OAPE+
OAPE+![]() ODPF,代入数值即可求得结果.
ODPF,代入数值即可求得结果.
连接OP,如图所示:
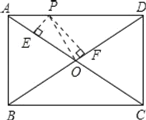
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,∠ABC=90°,
BD,∠ABC=90°,
S△AOD=![]() S矩形ABCD,
S矩形ABCD,
∴OA=OD=![]() AC,
AC,
∵AB=15,BC=20,
∴AC=![]() =
=![]() =25,S△AOD=
=25,S△AOD=![]() S矩形ABCD=
S矩形ABCD=![]() ×15×20=75,
×15×20=75,
∴OA=OD=![]() ,
,
∴S△AOD=S△APO+S△DPO=![]() OAPE+
OAPE+![]() ODPF=
ODPF=![]() OA(PE+PF)=
OA(PE+PF)=![]() ×
×![]() (PE+PF)=75,
(PE+PF)=75,
∴PE+PF=12.
∴点P到矩形的两条对角线AC和BD的距离之和是12.
故选B.

练习册系列答案
相关题目