题目内容
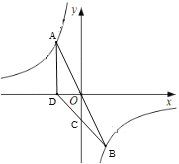
【题目】如图,直线y=﹣![]() x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
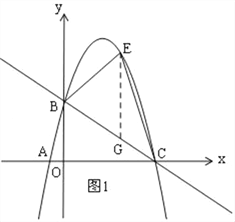
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
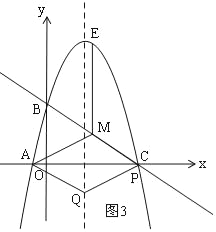
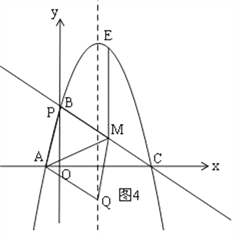
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)E(3,8);(3)点P的坐标是(﹣2,﹣
x+4;(2)E(3,8);(3)点P的坐标是(﹣2,﹣![]() )或(6,0)或(0,4).
)或(6,0)或(0,4).
【解析】试题分析:(1)首先根据直线![]() 与x轴交于点C,与y轴交于点B,求出点B的坐标是
与x轴交于点C,与y轴交于点B,求出点B的坐标是![]() ,点C的坐标是
,点C的坐标是![]() 然后根据抛物线
然后根据抛物线![]() 经过
经过![]() 两点,求出
两点,求出![]() 的值是多少,即可求出抛物线的解析式.
的值是多少,即可求出抛物线的解析式.
(2)首先过过E作EG∥y轴,交直线BC于G,然后设![]() 则
则![]() 求出
求出![]() 的值是多少;最后根据三角形的面积的求法,求出
的值是多少;最后根据三角形的面积的求法,求出![]() 进而判断出当
进而判断出当![]() 面积最大时,点E的坐标和
面积最大时,点E的坐标和![]() 面积的最大值各是多少即可.
面积的最大值各是多少即可.
(3)在抛物线上存在点P,使得以![]() 为顶点的四边形是平行四边形.然后分三种情况讨论,根据平行四边形的特征,求出使得以
为顶点的四边形是平行四边形.然后分三种情况讨论,根据平行四边形的特征,求出使得以![]() 为顶点的四边形是平行四边形的点P的坐标是多少即可.
为顶点的四边形是平行四边形的点P的坐标是多少即可.
试题解析:(1)当![]() 时,
时, ![]()
∴![]() ,
,
当![]() 时,
时, ![]()
![]() ∴
∴![]()
把![]() 和
和![]() 代入抛物线
代入抛物线![]() 中得:
中得:

解得:  ,
,
∴抛物线的解析式为: ![]()
(2)如图1,过E作EG∥y轴,交直线BC于G,
设![]() 则
则![]()
![]()
![]()
∵![]()
∴S有最大值,此时![]()
(3)![]()
对称轴是: ![]()
∴![]()
在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.
如图2,以AM为边时,由(2),可得点M的横坐标是3,
∵点M在直线![]() 上,
上,
∴点M的坐标是(3,2),
又∵点A的坐标是(﹣1,0),点Q的横坐标为2,
根据M到Q的平移规律:可知:P的横坐标为﹣2,
∴![]()
②如图3,以AM为边时,四边形AMPQ是平行四边形,
由(2),可得点M的横坐标是2,
∵A(﹣1,0),且Q的横坐标为2,
∴P的横坐标为6,
∴P(6,0)(此时P与C重合);
③以AM为对角线时,如图4,
∵M到Q的平移规律可得P到A的平移规律
∴点P的坐标是(0,4)
综上所述,在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,
点P的坐标是![]() 或(6,0)或(0,4).
或(6,0)或(0,4).


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】2013年安庆市体育考试跳绳项目为学生选考项目,下表是某班模拟考试时10名同学的测试成绩(单位:个/分钟),则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
A. 众数是177 B. 平均数是170 C. 中位数是173.5 D. 方差是135
【题目】某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定,现从两家提供的样品中各抽取了6件进行检查,超过标准质量部分记为正数,不足部分记为负数,若该皮具的标准质量为500克,测得它们质量如下(单位:g)
厂家 | 超过标准质量的部分 | |||||
甲 | ﹣3 | 0 | 0 | 1 | 2 | 0 |
乙 | ﹣2 | 1 | ﹣1 | 0 | 1 | 1 |
(1)分别计算甲、乙两厂抽样检测的皮具总质量各是多少克?
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?
【题目】某新店开业宣传,进店有礼活动,店员们需准备制作圆柱体礼品纸盒(如图①),每个纸盒由1个长方形侧面和2个圆形底面组成,现有100张正方形纸板全部以A或者B方法截剪制作(如图②),设截剪时x张用A方法.
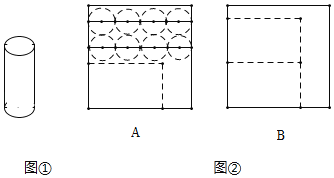
(1)根据题意,完成以下表格:
裁剪法A | 裁剪法B | |
长方形侧面 | x |
|
圆形底面 |
| 0 |
(2)若裁剪出的长方形侧面和圆形底面恰好用完,问能做多少个纸盒?
(3)按以上制作方法,若店员们希望准备300个礼盒,那至少还需要正方形纸板 张.