题目内容
【题目】阅读下面材料
在数学课上，老师提出如下问题:
己知:已知:Rt△ABC,∠ABC=90°.
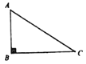
求作:矩形ABCD.
小敏的作法如下:
①以A为圆心，BC长为半径作弧，以C为圆心，AB长为半径作弧，两弧相交于点D;
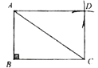
②连接DA、DC;所以四边形ABCD为所求矩形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是____________________.
【答案】有一个角是直角的平行四边形是矩形
【解析】
直接利用基本作图方法得出四边形ABCD是平行四边形，进而利用矩形的判定方法得出答案．
①以A为圆心，BC长为半径作弧，以C为圆心，AB长为半径作弧，两弧相交于点D；
②连接DA、DC；所以四边形ABCD为所求矩形．
理由：∵AD=BC，AB=DC，
∴四边形ABCD是平行四边形，
∵∠B=90°，
∴平行四边形ABCD是矩形．
故答案为：有一个角是直角的平行四边形是矩形．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
