题目内容
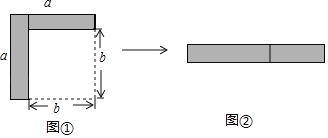
【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
【答案】B
【解析】分析:
用含“a、b”的式子分别表达出图①中阴影部分的面积和图②的面积,两者进行对比即可得到结论.
详解:
由图形①可知剪掉后剩下的图形面积是:a2-b2,
由题意可得:图形②的长为(a+b),宽为(a﹣b),
∴图形②的面积是:(a+b)(a﹣b),
又∵由题意可知,图形①中剩下部分的面积和图形②的面积相等,
∴a2-b2 =(a+b)(a﹣b)
故选B.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目