题目内容
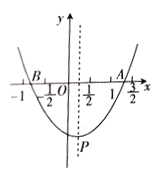
【题目】在直角坐标系XOY中,二次函数图像的顶点坐标为![]() ,且与x轴的两个交点间的距离为6.
,且与x轴的两个交点间的距离为6.
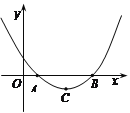
(1)求二次函数解析式;
(2)在x轴上方的抛物线上,是否存在点Q,使得以点Q、A、B为顶点的三角形与△ABC相似?如果存在,请求出Q点的坐标,如果不存在,请说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() 或
或![]()
【解析】
(1)由已知开设解析式:![]() ,B(7,0),进一步可求出结果;(2)过点O作CD⊥x轴于D,过点Q作QE⊥x轴于E,利用三角函数求出E,Q坐标,证明点Q在抛物线上,由抛物线的对称性,还存在一点
,B(7,0),进一步可求出结果;(2)过点O作CD⊥x轴于D,过点Q作QE⊥x轴于E,利用三角函数求出E,Q坐标,证明点Q在抛物线上,由抛物线的对称性,还存在一点![]() ,使△ABQ′∽△CAB.
,使△ABQ′∽△CAB.
(1)由已知开设解析式:![]() ,B(7,0)
,B(7,0)
把B(7,0)代入,求得a=![]()
故所求解析式为![]()
(2)在x轴上方的抛物线上存在点Q,使得以点Q、A、B为顶点的三角形与△ABC相似,
因为△ABC为等腰三角形,
∴当AB=BQ,
∵AB=6,
∴BQ=6,
过点O作CD⊥x轴于D,则AD=3,CD=![]() ,
,
∴∠BAC=∠ABC=30°,∴∠ACB=120°,∴∠ABQ=120°,
过点Q作QE⊥x轴于E,则∠QBE=60°,
∴QE=BQsin60°=![]() ,
,
∴BE=3,
∴E(10, 0),![]() .
.
当x=10时,![]()
∴点Q在抛物线上,
由抛物线的对称性,还存在一点![]() ,
,
使△ABQ′∽△CAB故存在点![]() 或
或![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目