题目内容
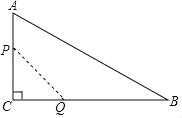
【题目】如图,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高,则下列结论:①. ∠BCD=60°;②. 四边形EHCF为菱形;③ ![]() ;
;
④. 以AB为直径的圆与CD相切于点F.其中正确的个数是( )
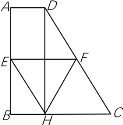
A.1B.2C.3D.4
【答案】C
【解析】
在直角三角形CDH中,CH=BC-BH,而四边形ABHD是矩形,故AD=BH,从而可求CH,利用30°角的性质可求∠CDH=30°,进而可求∠DCB的值;再利用梯形中位线定理可证四边形EHCF是菱形;△BEH与△EHC时等高的两个三角形,求面积比,也就是求底边的比,即BH:CH;在△CDH中利用勾股定理,可求DH,即AB的值,用其一半与EF比较,相等则切于F,否则不成立.
解:在Rt△DCH中,CD=4,CH=CB-BH=2,
∴∠CDH=30°,
∴∠BCD=60°,故①正确;
在四边形EHCF中,
∵EF为梯形的中位线,
∴CH=EF=2,CH∥EF,CF=![]() CD=2,
CD=2,
∴四边形EHCF为平行四边形,
∵CH=CF=2,
∴四边形EHCF是菱形,故②正确;
∵S△BEH=![]() BHEB=
BHEB=![]() ×1×EB=
×1×EB=![]() EB,
EB,
S△CEH=![]() CHEB=
CHEB=![]() ×2×EB=EB,
×2×EB=EB,
∴S△BEH=![]() S△CEH.故③正确;
S△CEH.故③正确;
以AB的直径的圆的半径为![]() ,而EF=2,R≠EF.所以AB为直径的圆与CD不相切于点F.故④不正确;
,而EF=2,R≠EF.所以AB为直径的圆与CD不相切于点F.故④不正确;
故选C.

练习册系列答案
相关题目