题目内容
【题目】如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.
(1)求AD的长.
(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.

【答案】(1)AD=2![]() ;(2)当△DPF是等腰三角形时,AP的长为0或5或8﹣2
;(2)当△DPF是等腰三角形时,AP的长为0或5或8﹣2![]() .
.
【解析】
(1)先求出AC,进而求出AE=4,再用勾股定理求出DE即可得出结论;
(2)分三种情况,利用相似三角形得出比例式,即可得出结论
(1)如图1,连接OD,
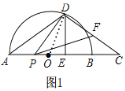
∵OA=OD=3,BC=2,
∴AC=8,
∵DE是AC的垂直平分线,
∴AE=![]() AC=4,
AC=4,
∴OE=AE﹣OA=1,
在Rt△ODE中,DE=![]() =2
=2![]() ;
;
在Rt△ADE中,AD=![]() =2
=2![]() ;
;
(2)当DP=DF时,如图2,

点P与A重合,F与C重合,则AP=0;
当DP=PF时,如图4,
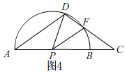
∴∠CDP=∠PFD,
∵DE是AC的垂直平分线,∠DPF=∠DAC,
∴∠DPF=∠C,
∵∠PDF=∠CDP,
∴△PDF∽△CDP,
∴∠DFP=∠DPC,
∴∠CDP=∠CPD,
∴CP=CD,
∴AP=AC﹣CP=AC﹣CD=AC﹣AD=8﹣2![]() ;
;
当PF=DF时,如图3,

∴∠FDP=∠FPD,
∵∠DPF=∠DAC=∠C,
∴△DAC∽△PDC,
∴![]() ,
,
∴![]() ,
,
∴AP=5,
即:当△DPF是等腰三角形时,AP的长为0或5或8﹣2![]() .
.

练习册系列答案
相关题目