题目内容
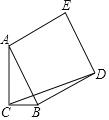
【题目】已知:如图,在菱形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 与
与![]() 满足什么关系时,四边形
满足什么关系时,四边形![]() 是正方形?请说明理由.
是正方形?请说明理由.
【答案】见解析
【解析】
(1)由菱形的性质得出∠B=∠D,AB=BC=DC=AD,由已知和三角形中位线定理证出AE=BE=DF=AF,OF=![]() DC,OE=
DC,OE=![]() BC,OE∥BC,由(SAS)证明△BCE≌△DCF即可;
BC,OE∥BC,由(SAS)证明△BCE≌△DCF即可;
(2)由(1)得:AE=OE=OF=AF,证出四边形AEOF是菱形,再证出∠AEO=90°,四边形AEOF是正方形.
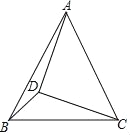
(1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD,
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF,OF=![]() DC,OE=
DC,OE=![]() BC,OE∥BC,
BC,OE∥BC,
在△BCE和△DCF中,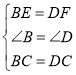 ,
,
∴△BCE≌△DCF(SAS);
(2)当AB⊥BC时,四边形AEOF是正方形,理由如下:
由(1)得:AE=OE=OF=AF,
∴四边形AEOF是菱形,
∵AB⊥BC,OE∥BC,
∴OE⊥AB,
∴∠AEO=90°,
∴四边形AEOF是正方形.

【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,为迎接第
个世界读书日,为迎接第![]() 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按![]() 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
【题目】某公司招聘一名员工,现有甲、乙两人竞聘,公司聘请了3位专家和4位群众代表组成评审组,评审组对两人竟聘演讲进行现场打分,记分采用100分制,其得分如下表:
评委(序号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲(得分) | 89 | 94 | 93 | 87 | 95 | 92 | 87 |
乙(得分) | 87 | 89 | 91 | 95 | 94 | 96 | 89 |
(1)甲、乙两位竞聘者得分的中位数分别是多少
(2)计算甲、乙两位应聘者平均得分,从平均得分看应该录用谁(结果保留一位小数)
(3)现知道1、2、3号评委为专家评委,4、5、6、7号评委为群众评委,如果对专家评委组与群众评委组的平均分数分别赋子适当的权,那么对专家评委组赋的权至少为多少时,甲的平均得分比乙的平均得分多0.5分及以上
【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.