题目内容
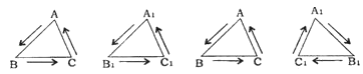
【题目】如图,二次函数y=x2﹣3x的图象经过O(0,0),A(4,4),B(3,0)三点,以点O为位似中心,在y轴的右侧将△OAB按相似比2:1放大,得到△OA′B′,二次函数y=ax2+bx+c(a≠0)的图象经过O,A′,B′三点.
(1)画出△OA′B′,试求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)点P(m,n)在二次函数y=x2﹣3x的图象上,m≠0,直线OP与二次函数y=ax2+bx+c(a≠0)的图象交于点Q(异于点O).
①连接AP,若2AP>OQ,求m的取值范围;
②当点Q在第一象限内,过点Q作QQ′平行于x轴,与二次函数y=ax2+bx+c(a≠0)的图象交于另一点Q′,与二次函数y=x2﹣3x的图象交于点M,N(M在N的左侧),直线OQ′与二次函数y=x2﹣3x的图象交于点P′.△Q′P′M∽△QB′N,则线段 NQ的长度等于 .

【答案】(1)二次函数的解析式为y=![]() x2﹣3x;(2)①1﹣
x2﹣3x;(2)①1﹣![]() <m<1+
<m<1+![]() ,且m≠0;②6
,且m≠0;②6
【解析】
(1)根据位似的性质得出A′(8,8),B′(6,0),将O(0,0),A′(8,8),B′(6,0)代入y=ax2+bx+c,利用待定系数法进行求解即可得;
(2)①如图1,由P(m,n)在二次函数y=x2﹣3x的图象上,可得P(m,m2﹣3m),根据待定系数法易求得OP的解析是为y=(m﹣3)x,继而可求得Q(2m,2m2﹣6m),过点P作PC⊥x轴于点C,过点Q作QD⊥x轴于点D,证明△OCP∽△ODQ,可得OQ=2OP,然后根据2AP>OQ,可得AP>OP,从而可得关于m的不等式,解不等式即可得;
②如图2,P(m,m2﹣3m),Q(2m,2m2﹣6m),根据点Q在第一象限,可得m>3,QQ′的表达式是y=2m2﹣6m,解方程组 ,可得点Q′(6﹣2m,2m2﹣6m),继而可得OQ′的解析式为y=﹣mx,从而求得点P′(3﹣m,m2﹣3m),由QQ′与y=x2﹣3x交于点M、N,求出点M、N的坐标,再根据△Q′P′M∽△QB′N,根据相似三角形的性质可得关于的方程,解方程求出m的值即可得答案.
,可得点Q′(6﹣2m,2m2﹣6m),继而可得OQ′的解析式为y=﹣mx,从而求得点P′(3﹣m,m2﹣3m),由QQ′与y=x2﹣3x交于点M、N,求出点M、N的坐标,再根据△Q′P′M∽△QB′N,根据相似三角形的性质可得关于的方程,解方程求出m的值即可得答案.
(1)如图1,由以点O为位似中心,在y轴的右侧将△OAB按相似比2:1放大,
得![]() ,
,
∵A(4,4),B(3,0),
∴A′(8,8),B′(6,0),
将O(0,0),A′(8,8),B′(6,0)代入y=ax2+bx+c,
得 ,解得
,解得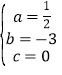 ,
,
∴二次函数的解析式为y=![]() x2﹣3x;
x2﹣3x;
(2)①如图1,∵P(m,n)在二次函数y=x2﹣3x的图象上,
∴n=m2﹣3m,
∴P(m,m2﹣3m),
设直线OP的解析式为y=kx,将点P(m,m2﹣3m)代入函数解析式,
得mk=m2﹣3m,
∴k=m﹣3,
∴OP的解析是为y=(m﹣3)x,
∵OP与y═![]() x2﹣3x交于Q点,
x2﹣3x交于Q点,
∴ ,解得
,解得![]() (不符合题意舍去),
(不符合题意舍去), ,
,
∴Q(2m,2m2﹣6m),
过点P作PC⊥x轴于点C,过点Q作QD⊥x轴于点D,
则OC=|m|,PC=|m2﹣3m|,OD=|2m|,QD=|2m2﹣6m|,
∵![]() ,
,
∴△OCP∽△ODQ,
∴OQ=2OP,
∵2AP>OQ,
∴2AP>2OP,即AP>OP,
∴![]() ,
,
化简,得m2﹣2m﹣4<0,解得1﹣![]() <m<1+
<m<1+![]() ,且m≠0;
,且m≠0;
②如图2,P(m,m2﹣3m),Q(2m,2m2﹣6m)
∵点Q在第一象限,
∴![]() ,解得m>3,
,解得m>3,
由Q(2m,2m2﹣6m),得QQ′的表达式是y=2m2﹣6m,
∵QQ′′交y=![]() x2﹣3x交于点Q′,
x2﹣3x交于点Q′,
 ,解得
,解得 (不符合题意,舍),
(不符合题意,舍), ,
,
∴Q′(6﹣2m,2m2﹣6m),
设OQ′的解析是为y=kx,(6﹣2m)k=2m2﹣6m,
解得k=﹣m,OQ′的解析式为y=﹣mx,
∵OQ′与y=x2﹣3x交于点P′,
∴﹣mx=x2﹣3x,
解得x1=0(舍),x2=3﹣m,
∴P′(3﹣m,m2﹣3m),
∵QQ′与y=x2﹣3x交于点M、N,
∴x2﹣3x=2m2﹣6m,
解得x1=![]() ,x2=
,x2=![]() ,
,
∵M在N左侧,
∴M(![]() ,2m2﹣6m),N(
,2m2﹣6m),N(![]() ,2m2﹣6m),
,2m2﹣6m),
∵△Q′P′M∽△QB′N,
∴![]() ,
,
∵![]() ,
,
即 ,
,
化简得:m2﹣12m+27=0,
解得:m1=3(舍),m2=9,
∴N(12,108),Q(18,108),
∴QN=6,
故答案为:6.