ЬтФПФкШн
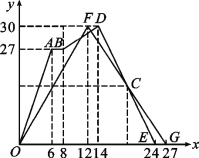
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЙ§AЃЈЉ3ЃЌ0ЃЉЁЂBЃЈ1ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЦфЖЅЕуЮЊDЃЌСЌНгADЃЌЕуPЪЧЯпЖЮADЩЯвЛИіЖЏЕуЃЈВЛгыAЁЂDжиКЯЃЉЃЌЙ§ЕуPзїyжсЕФДЙЯпPEЃЌДЙзуЕуЮЊEЃЌСЌНгAEЃЎ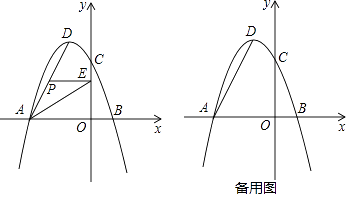
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЌВЂаДГіЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШчЙћPЕуЕФзјБъЮЊЃЈxЃЌyЃЉЃЌЁїPAEЕФУцЛ§ЮЊSЃЌЧѓSгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌжБНгаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБSШЁЕНзюДѓжЕЪБЃЌЙ§ЕуPзїxжсЕФДЙЯпPFЃЌДЙзуЮЊFЃЌСЌНгEFЃЌАбЁїPEFбижБЯпEFелЕўЃЌЕуPЕФЖдгІЕуЮЊЕуPЁфЃЌЧѓГіPЁфЕФзјБъЃЌВЂХаЖЯPЁфЪЧЗёдкИУХзЮяЯпЩЯЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКНЋЕуAКЭЕуBЕФзјБъДњШыЕУЃК ![]() ЃЌ
ЃЌ
НтЕУЃКa=1ЃЌb=Љ2ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2Љ2x+3ЃЎ
Ёпy=Љx2Љ2x+3=ЉЃЈx+1ЃЉ2+4ЃЌ
ЁрХзЮяЯпЕФЖЅЕузјБъЮЊDЮЊЃЈЉ1ЃЌ4ЃЉ
ЃЈ2ЃЉНтЃКЩшADЕФНтЮіЪНЮЊy=kx+bЃЌНЋЕуAКЭЕуDЕФзјБъДњШыЕУЃК ![]() ЃЌ
ЃЌ
НтЕУЃКk=2ЃЌb=6ЃЎ
ЁпPдкADЩЯЃЌ
ЁрPЃЈxЃЌ2x+6ЃЉЃЎ
ЁрS= ![]() PEyP=
PEyP= ![]() ЃЈЉxЃЉЃЈ2x+6ЃЉ=Љx2Љ3xЃЈЉ3ЃМxЃМЉ1ЃЉЃЎ
ЃЈЉxЃЉЃЈ2x+6ЃЉ=Љx2Љ3xЃЈЉ3ЃМxЃМЉ1ЃЉЃЎ
ЁрЕБx=Љ ![]() =Љ
=Љ ![]() ЪБЃЌSШЁжЕзюДѓжЕ
ЪБЃЌSШЁжЕзюДѓжЕ ![]()
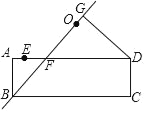
ЃЈ3ЃЉНтЃКШчЭМ1ЫљЪОЃКЩшPЁфFгыyжсНЛгыЕуNЃЌЙ§ЕуPЁфзїPЁфMЁЭyжсгыЕуMЃЎ
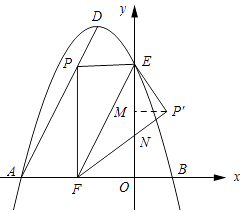
ЁпЕБx=Љ ![]() ЪБЃЌSШЁжЕзюДѓжЕЃЌ
ЪБЃЌSШЁжЕзюДѓжЕЃЌ
ЁрPЃЈЉ ![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ
гЩЗелЕФаджЪПЩжЊЃКЁЯPFE=ЁЯPЁфFEЃЌPF=PЁфF=3ЃЌPE=PЁфE= ![]() ЃЎ
ЃЎ
ЁпPFЁЮyжсЃЎ
ЁрЁЯPFE=ЁЯFENЃЎ
ЁрEN=FNЃЎ
ЩшEN=mЃЌдђFN=mЃЌPЁфN=3ЉmЃЎ
ЁпдкRtЁїPЁфENжаЃЌPЁфN2+PЁфE2=EN2ЃЌ
ЁрЃЈ3ЉmЃЉ2+ЃЈ ![]() ЃЉ2=m2ЃЌНтЕУЃКm=
ЃЉ2=m2ЃЌНтЕУЃКm= ![]() ЃЎ
ЃЎ
ЁпSЁїPЁфEN= ![]() PЁфNPЁфE=
PЁфNPЁфE= ![]() ENPЁфMЃЌ
ENPЁфMЃЌ
ЁрPЁфM= ![]() ЃЎ
ЃЎ
ЁпдкRtЁїEMPЁфжаЃЌEM= ![]() =
= ![]() ЃЌ
ЃЌ
ЁрOM=EOЉEM= ![]() ЃЎ
ЃЎ
ЁрPЁфЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
Абx= ![]() ДњШыХзЮяЯпЕФНтЮіЪНЕУЃКy=
ДњШыХзЮяЯпЕФНтЮіЪНЕУЃКy= ![]() Ёй
Ёй ![]() ЃЌ
ЃЌ
ЁрЕуPЁфВЛдкИУХзЮяЯпЩЯ
ЁОНтЮіЁПЃЈ1ЃЉгУД§ЖЈЯЕЪ§ЗЈНЋAЁЂBСНЕузјБъДњШыКЏЪ§НтЮіЪНМДПЩЧѓНтЃЌдйгУХфЗНЗЈЛђДњШыЖЅЕуЙЋЪНЧѓГіЖЅЕузјБъЁЃ
ЃЈ2ЃЉвЊЧѓЁїPAEЕУУцЛ§ЃЌгЩгкPEЁЭyжсЃЌЁїPAEЕУУцЛ§=![]() PE
PE![]() PEБпЩЯЕФИпЃЌвђДЫОЭЕУЧѓГіжБЯпADЕФКЏЪ§НтЮіЪНЃЌИљОнЕуPдкжБЯпADЩЯЃЌМДПЩгУКЌxЕФДњЪ§ЪНЧѓГіPEЁЂPEБпЩЯЕФИпЃЌМДПЩаДГіsгыx ЕФКЏЪ§ЙиЯЕЪНЃЌдйЧѓГіЖЅЕузјБъМДПЩЧѓЕУНсЙћЁЃ
PEБпЩЯЕФИпЃЌвђДЫОЭЕУЧѓГіжБЯпADЕФКЏЪ§НтЮіЪНЃЌИљОнЕуPдкжБЯпADЩЯЃЌМДПЩгУКЌxЕФДњЪ§ЪНЧѓГіPEЁЂPEБпЩЯЕФИпЃЌМДПЩаДГіsгыx ЕФКЏЪ§ЙиЯЕЪНЃЌдйЧѓГіЖЅЕузјБъМДПЩЧѓЕУНсЙћЁЃ
ЃЈ3ЃЉвЊЧѓЕуPЁфЕФзјБъЃЌЙ§ЕуPЁфзїPЁфMЁЭyжсгыЕуMЃЎгЩЃЈ2ЃЉЕУГіЕуPЕФзјБъЃЌИљОнелЕўЕФаджЪЃЌПЩвджЄЕУЁЯPFE=ЁЯPЁфFEЃЌPF=PЁфFЃЌPE=PЁфEЃЌдйжЄУїEN=FNЃЌдкRtЁїPЁфENжаЃЌдЫгУЙДЙЩЖЈРэЧѓГіENЕФГЄЃЌдйИљОнжБНЧШ§НЧаЮЕФУцЛ§ЕШгкСНжБНЧБпЛ§ЕФвЛАыЕШгкаББпГЫвдаББпЩЯЕФИпЃЌЧѓГіPЁфMЕФГЄЃЌдкRtЁїEMPЁфжаЧѓГіEMЕФГЄЃЌМДПЩЧѓЕУOMЕФГЄЃЌОЭПЩгУаДГіЕуPЁфЕФзјБъЃЌдйНЋЕуPЁфЕФКсзјБъДњШыКЏЪ§НтЮіЪНОЭПЩжЊЕРЕуPЁфЪЧЗёдкДЫХзЮяЯпЩЯЁЃ

 ИїЕиЦкФЉИДЯАЬибЕОэЯЕСаД№АИ
ИїЕиЦкФЉИДЯАЬибЕОэЯЕСаД№АИ аЁВЉЪПЦкФЉДГЙи100ЗжЯЕСаД№АИ
аЁВЉЪПЦкФЉДГЙи100ЗжЯЕСаД№АИ