题目内容
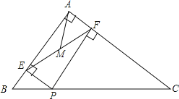
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


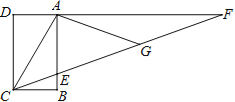
(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
【答案】(1)∠E、∠CAF;∠CDE、∠BAF; (2)①20°;②30
【解析】
(1)由翻折的性质和平行线的性质即可得与∠B相等的角;由等角代换即可得与∠C相等的角;
(2)①由三角形内角和定理可得![]() ,再由
,再由![]() 根据角的和差计算即可得∠C的度数,进而得∠B的度数.
根据角的和差计算即可得∠C的度数,进而得∠B的度数.
②根据翻折的性质和三角形外角及三角形内角和定理,用含x的代数式表示出∠FDE、∠DFE的度数,分三种情况讨论求出符合题意的x值即可.
(1)由翻折的性质可得:∠E=∠B,
∵∠BAC=90°,AE⊥BC,
∴∠DFE=90°,
∴180°-∠BAC=180°-∠DFE=90°,
即:∠B+∠C=∠E+∠FDE=90°,
∴∠C=∠FDE,
∴AC∥DE,
∴∠CAF=∠E,
∴∠CAF=∠E=∠B
故与∠B相等的角有∠CAF和∠E;
∵∠BAC=90°,AE⊥BC,
∴∠BAF+∠CAF=90°, ∠CFA=180°-(∠CAF+∠C)=90°
∴∠BAF+∠CAF=∠CAF+∠C=90°
∴∠BAF=∠C
又AC∥DE,
∴∠C=∠CDE,
∴故与∠C相等的角有∠CDE、∠BAF;
(2)①∵![]()
∴![]()
又∵![]() ,
,
∴∠C=70°,∠B=20°;
②∵∠BAD=x°, ∠B=20°则![]() ,
,![]() ,
,
由翻折可知:∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
当∠FDE=∠DFE时,![]() , 解得:
, 解得:![]() ;
;
当∠FDE=∠E时,![]() ,解得:
,解得:![]() (因为0<x≤45,故舍去);
(因为0<x≤45,故舍去);
当∠DFE=∠E时,![]() ,解得:
,解得:![]() (因为0<x≤45,故舍去);
(因为0<x≤45,故舍去);
综上所述,存在这样的x的值,使得△DEF中有两个角相等.且![]() .
.

 名校课堂系列答案
名校课堂系列答案