题目内容
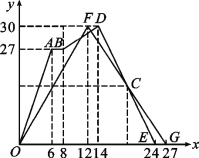
【题目】甲、乙两组同学玩“两人背夹球”比赛,即:每组两名同学用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲组两位同学掉了球;乙组两位同学顺利跑完.设比赛中同学距出发点的距离用y表示,单位是米;比赛时间用x表示,单位是秒.两组同学比赛过程用图像表示如下:
(1)这是一次 米的背夹球比赛;
(2)线段 表示甲组两位同学在比赛中途掉球,耽误了 秒;
(3)甲组同学到达终点用了 秒,乙组同学到达终点用了 秒,获胜的是 组同学;
(4)请直接写出C点坐标,并说明点C的实际意义.
【答案】(1)60;(2)AB,2;(3)24,27,甲;(4)C的坐标(18,18),点C的实际意义是当比赛进行到18秒时,甲组同学追上乙组同学,此时甲、乙两组同学离终点均为18米.
【解析】
(1)根据函数图象的纵坐标为30,可得这是一次60米的背夹球比赛;
(2)因为从A到B的路程不变,所以甲组两位同学在比赛中掉了球,因为从A到B的时间为2秒,所以耽误了2秒;
(3)利用横坐标可得,甲组同学用了24秒,乙组同学用了27秒,获胜的是甲组同学;
(4)根据点F,G的坐标,求出直线FG的函数解析式,根据点D,E的坐标,求出直线DE的函数解析式,然后组成方程组,求方程组的解,即为C的坐标,即可解答.
解:(1)根据函数图象可得这是一次60米的背夹球比赛;
(2)因为从A到B的路程不变,所以甲组两位同学在比赛中掉了球,因为从A到B的时间为2秒,所以线段AB表示甲组两位同学在比赛中掉了球,耽误了2秒;
(3)根据横坐标可知,甲组同学到达终点用了24秒,乙组同学到达终点用了27秒,获胜的是甲组同学;
(4)设直线FG的函数解析式为:y=k1x+b1,
把F(12,30),G(27,0)代入y=k1x+b1 得:
![]() ,
,
解得:![]() ,
,
∴直线FG的函数解析式为:y=-2x+54;
设直线DE的函数解析式为:y=k2x+b2,
把D(14,30),E(24,0)代入y=k2x+b2 得:
![]() ,
,
解得:![]() ,
,
∴直线DE的函数解析式为:y=-3x+72,
∴得到方程组![]() ,
,
解得:![]() ,
,
∴C的坐标(18,18),表示当比赛进行到18秒时,甲组同学追上乙组同学,此时甲、乙两组同学离终点均为18米.
故答案为:(1)60;(2)AB,2;(3)24,27,甲;(4)C的坐标(18,18),点C的实际意义是当比赛进行到18秒时,甲组同学追上乙组同学,此时甲、乙两组同学离终点均为18米.

【题目】如图所示的表格是某次篮球联赛部分球队的积分表,则下列说法不正确的是( )
队名 | 比赛场数 | 胜场 | 负场 | 积分 |
前进 | 14 | 10 | 4 | 24 |
光明 | 14 | 9 | 5 | 23 |
远大 | 14 | 7 | a | 21 |
卫星 | 14 | 4 | 10 | b |
钢铁 | 14 | 0 | 14 | 14 |
… | … | … | … | … |
A.负一场积1分,胜一场积2分B.卫星队总积分b=18
C.远大队负场数a=7D.某队的胜场总积分可以等于它的负场总积分