题目内容
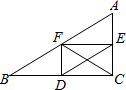 如图在△ABC中,BC=8,AC=6,AB=10,它们的中点分别是点D、E、F,则CF的长为________.
如图在△ABC中,BC=8,AC=6,AB=10,它们的中点分别是点D、E、F,则CF的长为________.
5
分析:利用勾股定理的逆定理可以推知∠ACB=90°;然后利用三角形中位线定理可以求得平行四边形CEFD是矩形、EF与CE的长度;最后在直角三角形DFC中利用勾股定理求得CF的长度.
解答: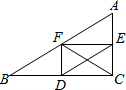 解:∵在△ABC中,BC=8,AC=6,AB=10,
解:∵在△ABC中,BC=8,AC=6,AB=10,
∴AB2=AC2+BC2,
∴∠ACB=90°;
又∵点D、E、F分别是BC、AC、AB的中点,
∴EF∥BC,且EF= BC=4,
BC=4,
FD∥AC,且FD= AC=3,
AC=3,
∴四边形CEFD是矩形,
∴EF=CD,
∴CF=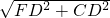 =5;
=5;
故答案是:5.
点评:本题综合考查了矩形的判定与性质、勾股定理的逆定理、三角形中位线定理.解答该题的突破口是根据已知条件“在△ABC中,BC=8,AC=6,AB=10”利用勾股定理的逆定理推知△ABC是直角三角形.
分析:利用勾股定理的逆定理可以推知∠ACB=90°;然后利用三角形中位线定理可以求得平行四边形CEFD是矩形、EF与CE的长度;最后在直角三角形DFC中利用勾股定理求得CF的长度.
解答:
 解:∵在△ABC中,BC=8,AC=6,AB=10,
解:∵在△ABC中,BC=8,AC=6,AB=10,∴AB2=AC2+BC2,
∴∠ACB=90°;
又∵点D、E、F分别是BC、AC、AB的中点,
∴EF∥BC,且EF=
 BC=4,
BC=4,FD∥AC,且FD=
 AC=3,
AC=3,∴四边形CEFD是矩形,
∴EF=CD,
∴CF=
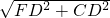 =5;
=5;故答案是:5.
点评:本题综合考查了矩形的判定与性质、勾股定理的逆定理、三角形中位线定理.解答该题的突破口是根据已知条件“在△ABC中,BC=8,AC=6,AB=10”利用勾股定理的逆定理推知△ABC是直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
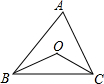 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,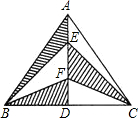 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是