题目内容
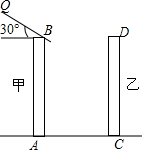
矩形ABCD中AE⊥BD于E，AB=4，∠BAE=30°，求△DEC的面积是______．
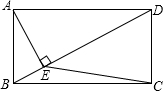
如图，过点C作CF⊥BD于F．
∵矩形ABCD中，AB=4，AE⊥BD，∠BAE=30°，
∴AB2=BE×BD，BE=2，AE=2
，
∴ED=BD-BE=6，
∴∠ABE=∠CDF=60°，AB=CD=4，AEB=∠CFD=90°．
∴△ABE≌△CDF．
∴AE=CF．
∴S△AED=
ED•AE，S△ECD=
ED•CF
∴S△AED=S△CDE，
∵AE=2
，DE=6，
∴△ECD的面积是6
．
故答案为：6
．
∵矩形ABCD中，AB=4，AE⊥BD，∠BAE=30°，
∴AB2=BE×BD，BE=2，AE=2
| 3 |
∴ED=BD-BE=6，
∴∠ABE=∠CDF=60°，AB=CD=4，AEB=∠CFD=90°．
∴△ABE≌△CDF．
∴AE=CF．
∴S△AED=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AED=S△CDE，
∵AE=2
| 3 |
∴△ECD的面积是6
| 3 |
故答案为：6
| 3 |
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
