题目内容
【题目】(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.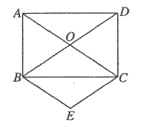
【答案】解(1)在矩形ABCD中,∠ABC=90°,
∴Rt△ABC中, ∠ACB=30°,
∴AC=2AB=4.
(2)在矩形ABCD中,
∴AO=OA=2,
又∵AB=2,
∴△AOB是等边三角形,
∴∠AOB=60°.
(3)由勾股定理,得BC=![]() ,
,
![]() .
.
![]() ,所以菱形OBEC的面积是2
,所以菱形OBEC的面积是2![]() .
.
【解析】
解 (1)在矩形ABCD中,∠ABC=90°,
∴Rt△ABC中, ∠ACB=30°,
∴AC=2AB=4.
(2)在矩形ABCD中,
∴AO=OA=2,
又∵AB=2,
∴△AOB是等边三角形,
∴∠AOB=60°.
(3)由勾股定理,得BC=![]() ,
,
![]() .
.
![]() ,所以菱形OBEC的面积是2
,所以菱形OBEC的面积是2![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目