题目内容
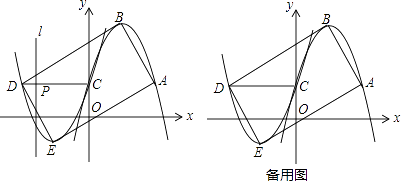
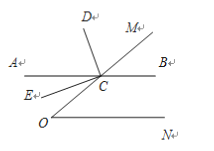
【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
【答案】(1)115°;(2)证明见解析;(3)结论:当∠O=36°或90°时,CA分∠OCD成1:2两部分.
【解析】(1)根据平行线的性质可得∠O=∠MCB,由平角定义可得∠ACM=130°,再利用角平分线的定义可求∠DCM=65°,从而可求出∠BCD的度数;
(2)利用等角的余角相等证明∠ACE=∠ECO即可;
(3)结合(2)的结论可知∠BOC=∠BOM=∠DOM,从而得出结论.
解:(1)∵AB∥ON,
∴∠O=∠MCB(两直线平行,同位角相等).
∵∠O=50°,
∴∠MCB=50°.
∵∠ACM+∠MCB=180°(平角定义),
∴∠ACM=180°-50°=130°.
又∵CD平分∠ACM,
∴∠DCM=65°(角平分线定义),
∴∠BCD=∠DCM+∠MCB=65°+50°=115°,
(2)∵CE⊥CD,
∴∠DCE=90°,
∴∠ACE+∠DCA=90°..
又∵∠MCO=180°(平角定义),
∴∠ECO+∠DCM=90°,
∵∠DCA =∠DCM,
∴∠ACE=∠ECO(等角的余角相等),
即CE平分∠OCA;
(3)①当∠OCA: ∠ACD=1:2时,
设∠OCD=x°, ∠ACD=2x°,由题意得
x+2x+2x=180,
∴x=36,
∴∠O=∠OCA=x=36°;
②当∠ACD:∠OCA =1:2时,
设∠ACD =x°, ∠OCA =2x°,由题意得
x+x+2x=180,
∴x=45,
∴∠O=∠OCA=2x=2×45°=90°;
∴当∠O=36°或90°时,CA分∠OCD成1:2两部分.

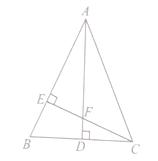
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

【题目】某公司要将一批货物运往某地,打算租用某汽车运输公司的甲.乙两种货车,以前租用这两种货车的信息如下表所示;
第一次 | 第二次 | |
甲种货车辆数/辆 | 2 | 5 |
乙种货车辆数/辆 | 3 | 6 |
累计运货量/吨 | 15.5 | 35 |
现打算租用该公司4辆甲种货车和6辆乙种货车,可一次刚好运完这批货物.如果每吨运费为50元,该公司应付运费________元.