Question

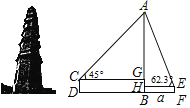
【题目】慈氏塔位于岳阳市城西洞庭湖边，是湖南省保存最好的古塔建筑之一.如图，小亮的目高CD为1.7米，他站在D处测得塔顶的仰角∠ACG为45°，小琴的目高EF为1.5米，她站在距离塔底中心B点a米远的F处，测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上，参考数据：sin62.3°≈0.89，cos62.3°≈0.46，tan62.3°≈1.9)

(1)求小亮与塔底中心的距离BD；(用含a的式子表示)

(2)若小亮与小琴相距52米，求慈氏塔的高度AB.

Answer 1

【答案】(1)小亮与塔底中心的距离BD(1.9a﹣0.2)米；(2)慈氏塔的高度AB为36.1米.

【解析】

(1)由题意得，四边形CDBG、HBFE为矩形，求得GH＝0.2，在Rt△AHE中，利用∠AEH的正切求得AH≈1.9a，从而得AG＝1.9a﹣0.2，在Rt△ACG中，根据等腰直角三角形的性质求得CG＝AG＝1.9a﹣0.2，由此即可求得答案；

(2)由题意可得关于a的方程，解方程求得a的值即可得答案.

(1)由题意得，四边形CDBG、HBFE为矩形，

∴GB＝CD＝1.7，HB＝EF＝1.5，

∴GH＝0.2，

在Rt△AHE中，tan∠AEH＝，

则AH＝HEtan∠AEH≈1.9a，

∴AG＝AH﹣GH＝1.9a﹣0.2，

在Rt△ACG中，∠ACG＝45°，

∴CG＝AG＝1.9a﹣0.2，

∴BD＝1.9a﹣0.2，

答：小亮与塔底中心的距离BD(1.9a﹣0.2)米；

(2)由题意得，1.9a﹣0.2+a＝52，

解得，a＝18，

则AG＝1.9a﹣0.2＝34.4，

∴AB＝AG+GB＝36.1，

答：慈氏塔的高度AB为36.1米.