题目内容
【题目】在![]() 中,
中,![]() ,以
,以![]() 为斜边作等腰直角
为斜边作等腰直角![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为______.
的长为______.
【答案】6或2.
【解析】
由于已知没有图形,当Rt△ABC固定后,根据“以BC为斜边作等腰直角△BCD”可知分两种情况讨论:
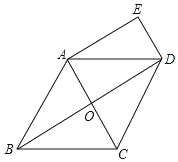
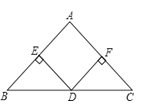
①当D点在BC上方时,如图1,把△ABD绕点D逆时针旋转90°得到△DCE,证明A、C、E三点共线,在等腰Rt△ADE中,利用勾股定理可求AD长;
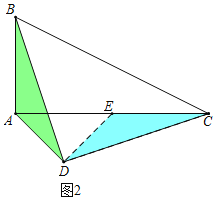
②当D点在BC下方时,如图2,把△BAD绕点D顺时针旋转90°得到△CED,证明过程类似于①求解.
解:分两种情况讨论:
①当D点在BC上方时,如图1所示,
把△ABD绕点D逆时针旋转90°,得到△DCE,
则∠ABD=∠ECD,CE=AB=2![]() ,AD=DE,且∠ADE=90°
,AD=DE,且∠ADE=90°
在四边形ACDB中,∠BAC+∠BDC=90°+90°=180°,
∴∠ABD+∠ACD=360°-180°=180°,
∴∠ACD+∠ECD=180°,
∴A、C、E三点共线.
∴AE=AC+CE=4![]() +2
+2![]() =6
=6![]()
在等腰Rt△ADE中,AD2+DE2=AE2,
即2AD2=(6![]() )2,解得AD=6
)2,解得AD=6

②当D点在BC下方时,如图2所示,
把△BAD绕点D顺时针旋转90°得到△CED,
则CE=AB=2![]() ,∠BAD=∠CED,AD=AE且∠ADE=90°,
,∠BAD=∠CED,AD=AE且∠ADE=90°,
所以∠EAD=∠AED=45°,
∴∠BAD=90°+45°=135°,即∠CED=135°,
∴∠CED+∠AED=180°,即A、E、C三点共线.
∴AE=AC-CE=4![]() -2
-2![]() =2
=2![]()
在等腰Rt△ADE中,2AD2=AE2=8,解得AD=2.
故答案为:6或2.

练习册系列答案
相关题目