Question

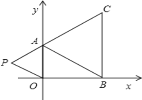
【题目】如图1，矩形的顶点、分别在轴与轴上，且点，点，点为矩形、两边上的一个点．

（1）当点与重合时，求直线的函数解析式；

（2）如图②，当在边上，将矩形沿着折叠，点对应点恰落在边上，求此时点的坐标．

（3）是否存在使为等腰三角形？若存在，直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=x+2；（2）（，10）；（3）存在， P坐标为（6，6）或（6，2+2）或（6，10-2）．

【解析】

（1）设直线DP解析式为y=kx+b，将D与C坐标代入求出k与b的值，即可确定出解析式；
（2）当点B的对应点B′恰好落在AC边上时，根据勾股定理列方程即可求出此时P坐标；
（3）存在，分别以BD，DP，BP为底边三种情况考虑，利用勾股定理及图形与坐标性质求出P坐标即可．

解：（1）∵C（6，10）,D（0，2），
设此时直线DP解析式为y=kx+b，
把D（0，2），C（6，10）分别代入，得
，
解得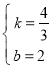
则此时直线DP解析式为y=x+2；
（2）设P（m，10），则PB=PB′=m，如图2，
∵OB′=OB=10，OA=6，
∴AB′==8，
∴B′C=10-8=2，
∵PC=6-m，
∴m2=22+（6-m）2，解得m=
则此时点P的坐标是（，10）；
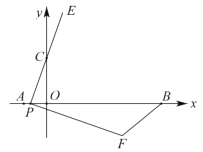
（3）存在，理由为：

若△BDP为等腰三角形，分三种情况考虑：如图3，
①当BD=BP1=OB-OD=10-2=8，
在Rt△BCP1中，BP1=8，BC=6，
根据勾股定理得：CP1=，
∴AP1=10-2，即P1（6，10-2）；
②当BP2=DP2时，此时P2（6，6）；
③当DB=DP3=8时，
在Rt△DEP3中，DE=6，
根据勾股定理得：P3E=，
∴AP3=AE+EP3=2+2，即P3（6，2+2），
综上，满足题意的P坐标为（6，6）或（6，2+2）或（6，10-2）．