题目内容
【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.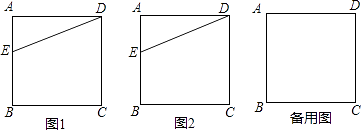
(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
【答案】
(1)解:如图所示:
依题意补全图形如图1:

(2)解:结论:BD⊥EG.
证明:如图2,BD,EG交于M,

∵正方形ABCD,
∴AB=BC,∠DAE=∠DCB=90°,
由旋转可得△ADE≌△CDF,DE=DF,AE=CF
∴∠DCF=∠DAE=∠DCB=90°,
∴点B,C,F在一条直线上.
∵点G与点F关于CD的对称
∴△DCG≌△DCF,DG=DF,CG=CF
∴DE=DG,AE=CG,
∴BE=BG
∴BD⊥EG于M.
(3)解:如图3,过G作GM⊥DE于M,

由(2)知,DE=DG,
设BE=x,
∴AE=CF=CG=BG=x,
∴AD=2x,
在Rt△ADE中,DE= ![]() =
= ![]() x,
x,
∴DG= ![]() x,
x,
在Rt△BEG中,EG= ![]() x,
x,
设DM=a,
∴EM=DE﹣DM= ![]() x﹣a,
x﹣a,
在Rt△EMG中,MG2=EG2﹣EM2,
∴MG2=2x2﹣( ![]() x﹣a)2,
x﹣a)2,
在Rt△DMG中,MG2=5x2﹣a2,
∴2x2﹣( ![]() x﹣a)2=5x2﹣a2,
x﹣a)2=5x2﹣a2,
∴a= ![]() ,
,
∴MG= ![]() x
x
在Rt△DMG中,tan∠EDG= ![]() =
= ![]() .
.
即:∠EDG的正切值为 ![]() .
.
【解析】(1)根据旋转中心旋转方向旋转角度画出图形即可;(2)先利用旋转判断出B、C、F在一条直线上,进而利用轴对称得出△DCG≌△DCF即可;(3)过G作GM⊥DE于M,构造出直角三角形,再利用勾股定理即可表示出GM、DM即可得出结论。
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
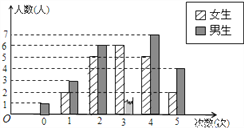
芒果教辅暑假天地重庆出版社系列答案【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
【题目】某超市投入1380元资金购进甲、乙两种矿泉水共50箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该超市购进甲、乙两种矿泉水各多少箱?
(2)全部售完50箱矿泉水,该超市共获得利润多少元?


