题目内容
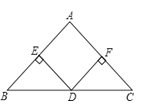
【题目】如图,在等腰Rt△ABC中,∠A=90°,点D是BC边上的中点,DE⊥AB于点E,DF⊥AC于点F.求证:四边形AEDF是正方形.
【答案】见详解
【解析】
由于AB=AC,那么∠B=∠C,而DE⊥AB,DF⊥AC可知∠BED=∠CFD=90°,又∵D是BC中点,可知BD=CD,利用AAS可证△BED≌△CFD,从而有DE=DF.再由∠AED=∠AFD=∠A=90°可知四边形AEDF为矩形,从而可得四边形AEDF为正方形.
证明:∵在等腰Rt△ABC中,∠A=90°,
∴AB=AC,
∴∠B=∠C,
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=∠AED=∠AFD=90°,
又∵D是BC中点,
∴BD=CD,
在△BED与△CFD中,
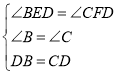
∴△BED≌△CFD(AAS),
∴DE=DF.
∵∠A=∠AED=∠AFD=90°
∴四边形AEDF为矩形,
又∵DE=DF,
∴矩形AEDF为正方形.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目