ЬтФПФкШн
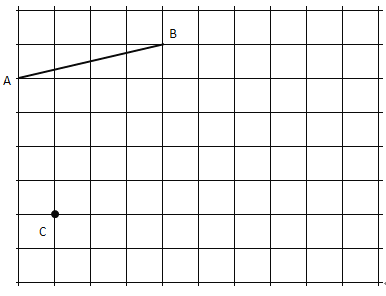
ЁОЬтФПЁПЮвУЧжЊЕРЃЌЦНУцФкЛЅЯрДЙжБЧвгаЙЋЙВдЕуЕФСНЬѕЪ§жсЙЙГЩЦНУцжБНЧзјБъЯЕЃЌШчЙћСНЬѕЪ§жсВЛДЙжБЃЌЖјЪЧЯрНЛГЩШЮвтЕФНЧІиЃЈ0ЁуЃМІиЃМ180ЁуЧвІиЁй90ЁуЃЉЃЌФЧУДетСНЬѕЪ§жсЙЙГЩЕФЪЧЦНУцаБзјБъЯЕЃЌСНЬѕЪ§жсГЦЮЊаБзјБъЯЕЕФзјБъжсЃЌЙЋЙВдЕуГЦЮЊаБзјБъЯЕЕФдЕуЃЌШчЭМ1ЃЌОЙ§ЦНУцФквЛЕуPзїзјБъжсЕФЦНааЯпPMКЭPNЃЌЗжБ№НЛxжсКЭyжсгкЕуMЃЌNЃЎЕуMЁЂNдкxжсКЭyжсЩЯЫљЖдгІЕФЪ§ЗжБ№НазіPЕуЕФxзјБъКЭyзјБъЃЌгаађЪЕЪ§ЖдЃЈxЃЌyЃЉГЦЮЊЕуPЕФаБзјБъЃЌМЧЮЊPЃЈxЃЌyЃЉЃЎ
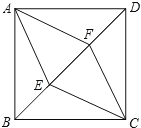
ЃЈ1ЃЉШчЭМ2ЃЌІиЃН45ЁуЃЌОиаЮOABCжаЕФвЛБпOAдкxжсЩЯЃЌBCгыyжсНЛгкЕуDЃЌOAЃН2ЃЌOCЃНlЃЎ
ЂйЕуAЁЂBЁЂCдкДЫаБзјБъЯЕФкЕФзјБъЗжБ№ЮЊAЁЁ ЁЁЃЌBЁЁ ЁЁЃЌCЁЁ ЁЁЃЎ
ЂкЩшЕуPЃЈxЃЌyЃЉдкОЙ§OЁЂBСНЕуЕФжБЯпЩЯЃЌдђyгыxжЎМфТњзуЕФЙиЯЕЮЊЁЁ ЁЁЃЎ
ЂлЩшЕуQЃЈxЃЌyЃЉдкОЙ§AЁЂDСНЕуЕФжБЯпЩЯЃЌдђyгыxжЎМфТњзуЕФЙиЯЕЮЊЁЁ ЁЁЃЎ
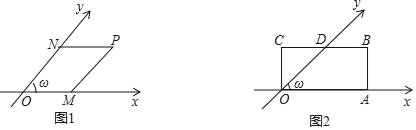
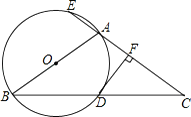
ЃЈ2ЃЉШєІиЃН120ЁуЃЌOЮЊзјБъдЕуЃЎ
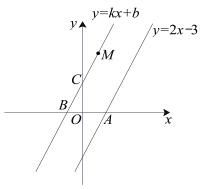
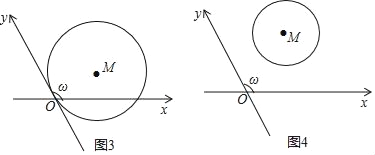
ЂйШчЭМ3ЃЌдВMгыyжсЯрЧадЕуOЃЌБЛxжсНиЕУЕФЯвГЄOAЃН4![]() ЃЌЧѓдВMЕФАыОЖМАдВаФMЕФаБзјБъЃЎ
ЃЌЧѓдВMЕФАыОЖМАдВаФMЕФаБзјБъЃЎ
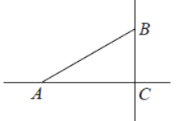
ЂкШчЭМ4ЃЌдВMЕФдВаФаБзјБъЮЊMЃЈ2ЃЌ2ЃЉЃЌШєдВЩЯЧЁгаСНИіЕуЕНyжсЕФОрРыЮЊ1ЃЌдђдВMЕФАыОЖrЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЃЈ2ЃЌ0ЃЉЃЌЃЈ1ЃЌ![]() ЃЉЃЌЃЈЉ1ЃЌ
ЃЉЃЌЃЈЉ1ЃЌ![]() ЃЉЃЛЂкy=
ЃЉЃЛЂкy=![]() xЃЛЂл y=
xЃЛЂл y=![]() xЃЌy=Љ
xЃЌy=Љ![]() x+
x+![]() ЃЛЃЈ2ЃЉЂйАыОЖЮЊ4ЃЌMЃЈ
ЃЛЃЈ2ЃЉЂйАыОЖЮЊ4ЃЌMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЂк
ЃЉЃЛЂк![]() Љ1ЃМrЃМ
Љ1ЃМrЃМ![]() +1ЃЎ
+1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйШчЭМ2-1жаЃЌзїBEЁЮODНЛOAгкEЃЌCFЁЮODНЛxжсгкFЃЎЧѓГіOEЁЂOFЁЂCFЁЂODЁЂBEМДПЩНтОіЮЪЬтЃЛЂкШчЭМ2-2жаЃЌзїBEЁЮODНЛOAгкEЃЌзїPMЁЮODНЛOAгкMЃЎРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэМДПЩНтОіЮЪЬтЃЛЂлШчЭМ3-3жаЃЌзїQMЁЮOAНЛODгкMЃЎРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЂйШчЭМ3жаЃЌзїMFЁЭOAгкFЃЌзїMNЁЮyжсНЛOAгкNЃЎНтжБНЧШ§НЧаЮМДПЩНтОіЮЪЬтЃЛЂкШчЭМ4жаЃЌСЌНгOMЃЌзїMKЁЮxжсНЛyжсгкKЃЌзїMNЁЭOKгкNНЛЁбMгкEЁЂFЃЎЧѓГіFN=NE=1ЪБЃЌЁбMЕФАыОЖМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉЂйШчЭМ2Љ1жаЃЌзїBEЁЮODНЛOAгкEЃЌCFЁЮODНЛxжсгкFЃЌ
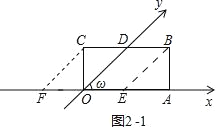
гЩЬтвтOC=CD=1ЃЌOA=BC=2ЃЌ
ЁрBD=OE=1ЃЌOD=CF=BE=![]() ЃЌ
ЃЌ
ЁрAЃЈ2ЃЌ0ЃЉЃЌBЃЈ1ЃЌ![]() ЃЉЃЌCЃЈЉ1ЃЌ
ЃЉЃЌCЃЈЉ1ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪД№АИЮЊЃЈ2ЃЌ0ЃЉЃЌЃЈ1ЃЌ![]() ЃЉЃЌЃЈЉ1ЃЌ
ЃЉЃЌЃЈЉ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкШчЭМ2Љ2жаЃЌзїBEЁЮODНЛOAгкEЃЌзїPMЁЮODНЛOAгкMЃЌ
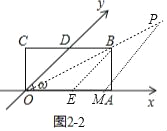
ЁпODЁЮBEЃЌODЁЮPMЃЌ
ЁрBEЁЮPMЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрy=![]() xЃЛ
xЃЛ
ЂлШчЭМ2Љ3жаЃЌзїQMЁЮOAНЛODгкMЃЌ
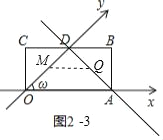
дђга![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрy=Љ![]() x+
x+![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊy=![]() xЃЌy=Љ
xЃЌy=Љ![]() x+
x+![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйШчЭМ3жаЃЌзїMFЁЭOAгкFЃЌзїMNЁЮyжсНЛOAгкNЃЌ
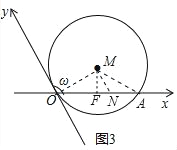
ЁпІи=120ЁуЃЌOMЁЭyжсЃЌ
ЁрЁЯMOA=30ЁуЃЌ
ЁпMFЁЭOAЃЌOA=4![]()
![]() ЃЌ
ЃЌ
ЁрOF=FA=2![]()
![]() ЃЌ
ЃЌ
ЁрFM=2ЃЌOM=2FM=4ЃЌ
ЁпMNЁЮyжсЃЌ
ЁрMNЁЭOMЃЌ
ЁрMN=![]() ЃЌON=2MN=
ЃЌON=2MN=![]() ЃЌ
ЃЌ
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкШчЭМ4жаЃЌСЌНгOMЃЌзїMKЁЮxжсНЛyжсгкKЃЌзїMNЁЭOKгкNНЛЁбMгкEЁЂFЃЎ
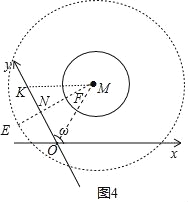
ЁпMKЁЮxжсЃЌІи=120ЁуЃЌ
ЁрЁЯMKO=60ЁуЃЌ
ЁпMK=OK=2ЃЌ
ЁрЁїMKOЪЧЕШБпШ§НЧаЮЃЌ
ЁрMN=![]() ЃЌ
ЃЌ
ЕБFN=1ЪБЃЌMF=![]() Љ1ЃЌ
Љ1ЃЌ
ЕБEN=1ЪБЃЌME=![]() +1ЃЌ
+1ЃЌ
ЙлВьЭМЯѓПЩжЊЕБЁбMЕФАыОЖrЕФШЁжЕЗЖЮЇЮЊ![]() Љ1ЃМrЃМ
Љ1ЃМrЃМ![]() +1ЃЎ
+1ЃЎ
ЙЪД№АИЮЊЃК![]() Љ1ЃМrЃМ
Љ1ЃМrЃМ![]() +1ЃЎ
+1ЃЎ

 жаПМРћНЃжаПМЪдОэЛуБрЯЕСаД№АИ
жаПМРћНЃжаПМЪдОэЛуБрЯЕСаД№АИ НЬг§ЪРМвзДдЊОэЯЕСаД№АИ
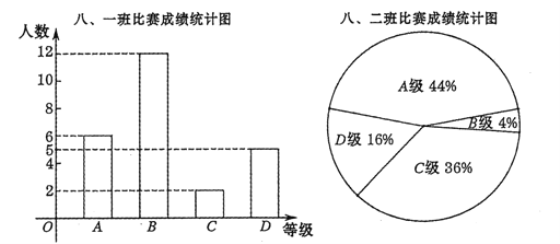
НЬг§ЪРМвзДдЊОэЯЕСаД№АИЁОЬтФПЁПФГаЃаЫШЄаЁзщдкДДПЭМЮФъЛЊЛюЖЏжазщжЏСЫМЦЫуЛњБрГЬБШШќЃЌАЫФъМЖУПАрХЩ25УћбЇЩњВЮМгЃЌГЩМЈЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЫФИіЕШМЖЃЎЦфжаЯргІЕШМЖЕФЕУЗжвРДЮМЧЮЊ10ЗжЁЂ9ЗжЁЂ8ЗжЁЂ7ЗжЃЎНЋАЫФъМЖЕФвЛАрКЭЖўАрЕФГЩМЈећРэВЂЛцжЦГЩШчЯТЭГМЦЭМБэЃК
ЫФИіЕШМЖЃЎЦфжаЯргІЕШМЖЕФЕУЗжвРДЮМЧЮЊ10ЗжЁЂ9ЗжЁЂ8ЗжЁЂ7ЗжЃЎНЋАЫФъМЖЕФвЛАрКЭЖўАрЕФГЩМЈећРэВЂЛцжЦГЩШчЯТЭГМЦЭМБэЃК
АрМЖ | ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ | ЗНВю |
вЛАр | 8ЃЎ76 | 9 | 9 |
|
ЖўАр | 8ЃЎ76 | 8 | 10 |
|
ЧыИљОнБОбЇЦкЫљбЇЙ§ЕФЁЖЪ§ОнЕФЗжЮіЁЗЯрЙижЊЪЖЗжЮіЩЯЪіЪ§ОнЃЌАяжњМЦЫуЛњБрГЬРЯЪІбЁдёвЛИіАрМЖВЮМгаЃМЖБШШќЃЌВЂВћЪіФубЁдёЕФРэгЩЃЎ