题目内容
【题目】如图,已知经过点M(1,4)的直线y = kx+b(k≠0)与直线y = 2x-3平行.
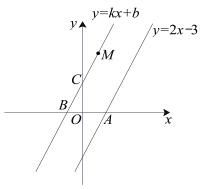
(1)求k,b的值;
(2)若直线y = 2x-3与x轴交于点A,直线y = kx+b交x轴于点B,交y轴于点C,求△MAC的面积.
【答案】(1)k = 2,b= 2;(2)2.5
【解析】
(1)先根据两直线平行得到k=2,然后把M点坐标代入y=2x+b求出b即可;
(2)求得A、B、C的坐标,然后根据S△MAC=S△AMB﹣S△ABC求得即可.
(1)∵ 直线y = kx+b(k≠0)与直线y = 2x-3平行,
∴ k = 2.
∵ 直线y = 2x+b经过点M(1,4),
∴ 2×1+b=4,
∴ b= 2.
∴ k = 2,b= 2
(2)连接AC,AM,
在直线y=2x-3中,
当y=0时,2x– 3 = 0,
解得x=1.5.
∴ 点A坐标是(1.5,0)
在y=2x+ 2中,
当y=0时,2x+ 2 = 0,
解得x=-1.
当x=0时,y= 2,
∴ 点B的坐标是(-1,0),点C的坐标是(0,2).
∴ AB=OA+OB =1.5+![]() =2.5
=2.5
∴ S△MAC =S△AMB -S△ABC
=![]() ×2.5×4 -
×2.5×4 -![]() ×2.5×2
×2.5×2
=2.5

 阅读快车系列答案
阅读快车系列答案【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具,共80个. 制作的道具需要甲、乙两种材料组合而成,现有甲种材料700件,乙种材料500件,已知组装A、B两种道具所需的甲、乙两种材料,如下表所示:
甲种材料(件) | 乙种材料(件) | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算,制作一个A道具的费用为5元,一个B道具的费用为4.5元. 设组装A种道具x个,所需总费用为y元.
(1)求y与x的函数关系式,并求出x的取值范围;
(2)问组装A种道具多少个时,所需总费用最少,最少费用是多少?
【题目】为了解黔东南州某县2013届中考学生的体育考试得分情况,从该县参加体育考试的4000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数分布直方图.
成绩分组 | 组中值 | 频数 |
25≤x<30 | 27.5 | 4 |
30≤x<35 | 32.5 | m |
35≤x<40 | 37.5 | 24 |
40≤x<45 | a | 36 |
45≤x<50 | 47.5 | n |
50≤x<55 | 52.5 | 4 |
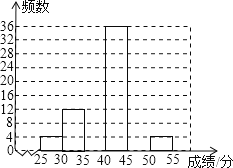
(1)求a、m、n的值,并补全频数分布直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀学生人数约为多少?