题目内容
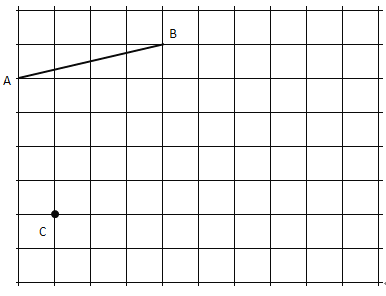
【题目】如图是10×8的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长都是1个单位,线段![]() 的端点均在格点上,且
的端点均在格点上,且![]() 点的坐标为
点的坐标为![]() ,按下列要求用没有刻度的直尺画出图形.
,按下列要求用没有刻度的直尺画出图形.
(1)请在图中找到原点![]() 的位置,并建立平面直角坐标系;
的位置,并建立平面直角坐标系;
(2)将线段![]() 平移到
平移到![]() 的位置,使
的位置,使![]() 与
与![]() 重合,画出线段
重合,画出线段![]() ,然后作线段
,然后作线段![]() 关于直线
关于直线![]() 对称线段
对称线段![]() ,使
,使![]() 的对应点为
的对应点为![]() ,画出线段
,画出线段![]() ;
;
(3)在图中找到一个各点![]() 使
使![]() ,画出
,画出![]() 并写出
并写出![]() 点的坐标.
点的坐标.
【答案】(1)见解析;(2)见解析;(3)见解析G(![]() )
)
【解析】
(1)根据A点坐标即可确定原点,建立平面直角坐标系;
(2)根据平移和轴对称的性质即可作图;
(3)连接AD,BC交于J,可得四边形ABCD为正方形,则AD⊥BC,延长AD至K,平移线段BC至EK,使B点跟E点重合,可得EH⊥AK与G点,再根据一次函数的图像与性质即可求出G点坐标.
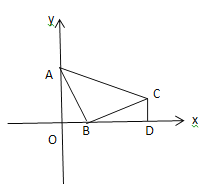
(1)如图所示,O点及坐标系为所求;
(2)如图,线段![]() ,线段
,线段![]() 为所求;
为所求;
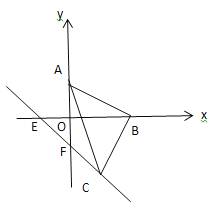
(3)如图,![]() 为所求,
为所求,
由直角坐标系可知A![]() ,D(3,2),故求得直线AD的解析式为:y=
,D(3,2),故求得直线AD的解析式为:y=![]() ;
;
由直角坐标系可知E![]() ,D(5,0),故求得直线AD的解析式为:y=
,D(5,0),故求得直线AD的解析式为:y= ![]() ;
;
联立两函数得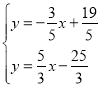 ,解得
,解得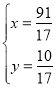
∴G(![]() ).
).


练习册系列答案
相关题目