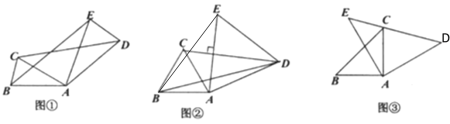
题目内容

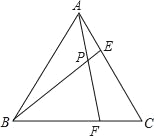
【题目】如图，等腰三角形的底边长为，面积是，腰的垂直平分线分别交，边于，点．若点为边的中点，点为线段上一动点，则周长的最小值为_________．

【答案】11

【解析】

连接AD，交EF于点M，根据的垂直平分线是可知CM=AM，求周长的最小值及求CM+DM的最小值，当A、M、D三点共线时，AM+AD最小，即周长的最小．

解：连接AD，交EF于点M，

∵△ABC为等腰三角形，点为边的中点，底边长为

∴AD⊥BC，CD=3

又∵面积是24，

即，

∴AD=8，

又∵的垂直平分线是，

∴AM=CM，

∴周长=CM+DM+CD= AM+DM+CD

∴求周长最小值即求AM+DM的最小值，

当A、M、D三点共线时，AM+AD最小，即周长的最小，

周长=AD+CD=8+3=11最小．

练习册系列答案
相关题目

【题目】如图所示，已知抛物线y=ax2+bx+c（a≠0）经过点A（﹣2，0）、B（4，0）、C（0，﹣8），与直线y=x﹣4交于B，D两点

（1）求抛物线的解析式并直接写出D点的坐标；

（2）点P为直线BD下方抛物线上的一个动点，试求出△BDP面积的最大值及此时点P的坐标；

（3）点Q是线段BD上异于B、D的动点，过点Q作QF⊥x轴于点F，交抛物线于点G，当△QDG为直角三角形时，直接写出点Q的坐标．

【题目】如图，△ABC和△ADE都是等腰直角三角形，CE与BD相交于点M，BD交AC于点N.

（1）证明：BD＝CE；

（2）证明：BD⊥CE．

【题目】如图，已知等边△ABC的边长为6，在AC，BC边上各取一点E，F，使AE=CF，连接AF、BE相交于点P，当点E从点A运动到点C时，点P经过点的路径长为__．

【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.

(1)求证:四边形ADEF是平行四边形;

(2)若∠ABC=60°,BD=6,求DE的长.

【题目】如图①，在正方形ABCD中，点E与点F分别在线段AC、BC上，且四边形DEFG是正方形．

（1）试探究线段AE与CG的关系，并说明理由．

（2）如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形，AB=3，BC=4．

①线段AE、CG在（1）中的关系仍然成立吗？若成立，请证明，若不成立，请写出你认为正确的关系，并说明理由．

②当△CDE为等腰三角形时，求CG的长．

【题目】如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．

求证：(1)FC＝AD；(2)AB＝BC+AD．

【题目】我们知道，平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系，如果两条数轴不垂直，而是相交成任意的角ω（0°＜ω＜180°且ω≠90°），那么这两条数轴构成的是平面斜坐标系，两条数轴称为斜坐标系的坐标轴，公共原点称为斜坐标系的原点，如图1，经过平面内一点P作坐标轴的平行线PM和PN，分别交x轴和y轴于点M，N．点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标，有序实数对（x，y）称为点P的斜坐标，记为P（x，y）．

（1）如图2，ω＝45°，矩形OABC中的一边OA在x轴上，BC与y轴交于点D，OA＝2，OC＝l．

①点A、B、C在此斜坐标系内的坐标分别为A　 　，B　 　，C　 　．

②设点P（x，y）在经过O、B两点的直线上，则y与x之间满足的关系为　 　．

③设点Q（x，y）在经过A、D两点的直线上，则y与x之间满足的关系为　 　．

（2）若ω＝120°，O为坐标原点．

①如图3，圆M与y轴相切原点O，被x轴截得的弦长OA＝4 ，求圆M的半径及圆心M的斜坐标．

②如图4，圆M的圆心斜坐标为M（2，2），若圆上恰有两个点到y轴的距离为1，则圆M的半径r的取值范围是　 　．

【题目】如图，和都是等腰三角形，其中，，且．

（1）如图①，连接、，求证：；

（2）如图②，连接、，若，，，，求的长；

（3）如图③，若，且点恰好落在上，试探究、和之间的数量关系，并加以说明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网