题目内容
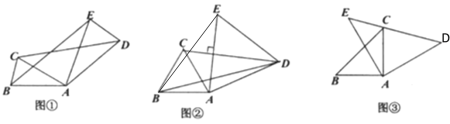
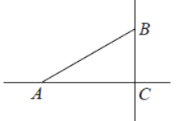
【题目】如图,![]() 中,
中,![]() ,
,![]() ,在直线
,在直线![]() 或
或![]() 上取一点
上取一点![]() ,使
,使![]() 为等腰三角形,则符合条件的点
为等腰三角形,则符合条件的点![]() 共有( )
共有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
分别以A为顶点、B为顶点、P为顶点讨论即可.
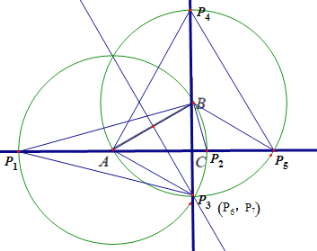
以点A为圆心,AB为半径作圆,交AC于P1,P2,交BC与P3,此时满足条件的等腰△PAB有3个;
以点B为圆心,AB为半径作圆,交AC于P5,交BC与P4,P6,此时满足条件的等腰△PAB有3个;
作AB的垂直平分线,交BC于P7,此时满足条件的等腰△PAB有1个;
∵![]() ,∴∠ABP3=60°,
,∴∠ABP3=60°,
∵AB=AP3,
∴△ABP3是等边三角形;
同理可证△ABP6,△ABP6是等边三角形,即△ABP3,△ABP6,△ABP7重合,
综上可知,满足条件的等腰△PAB有5个.
故选B.

练习册系列答案
相关题目