题目内容
【题目】如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.
(1)点C的坐标为__________;
(2)求证:△AFO≌△OEB;
(3)求证:∠ADO=∠EDB

【答案】(1)点C的坐标为(4,4);(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)先求出OA,OB进而求出OC,再用待定系数法求出直线AB的解析式,设出点C的坐标,即可得出结论;
(2)先判断出∠AOC=∠OBA,再利用互余判断出∠OAD=∠EOD,即可得出结论;
(3)先确定出OE的解析式,进而求出点E的坐标,即可求出直线DE的解析式,进而判断出OA=OM,即可得出结论.
试题解析:(1)A(0,8),B(0,8),
∴AB=8![]() ,OA=OB,
,OA=OB,
∴△AOB是等腰直角三角形,
∵OC是△AOB的中线,
∴OC=![]() AB=4
AB=4![]() ,
,
设直线AB的解析式为y=kx+b,
∵B(8,0),A(0,8),
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=-x+8,
设点C(m,-m+8),OC=![]() ,
,
∴m=4
∴C(4,4);
(2)由(1)知,OC是等腰直角三角形的斜边的中线,
∴∠AOC=45°=∠OBA,
∵OE⊥AD,
∴∠EOD+∠ODA=90°,
∵∠ADO+∠OAD=90°,
∴∠OAD=∠EOD,
在△AOF和△OBE中,
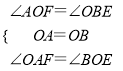 ,
,
∴△AOF≌△OBE;
(3)如图,
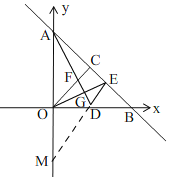
∵AD是△AOB的中线,
∴OD=BD,
∵B(8,0),
∴D(4,0),
∴直线AD的解析式为y=-2x+8,
∵OE⊥AD,
∴直线OE的解析式为y=![]() x,
x,
∵点E在直线AB上,
∴ ,解得,
,解得, 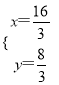 ,
,
∴E(![]() ,
, ![]() ),
),
∵D(4,0),
∴直线DE的解析式为y=2x-8,
∴OM=8,
∴OA=OM,
∵OB⊥OA,
∴AD=MD,
∴∠ADO=∠MDO.
∵∠EDB=∠MDO,
∴∠ADO=∠EDB.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案