题目内容
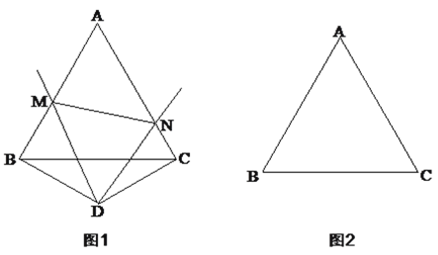
【题目】已知:△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60.
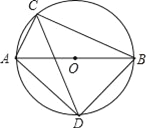
(1)如图1,当点D在△ABC外部时,求证:BM+CN=MN;
(2)在(1)的条件下求△AMN的周长;
(3)当点D在△ABC内部时,其它条件不变,请在图2中补全图形,并直接写出△AMN的周长.
【答案】(1)证明见解析;(2)6;(3)3.
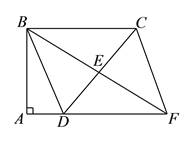
【解析】试题分析:(1)延长AB至F,使BF=CN,连接DF,只要证明△BDF≌△CND,△DMN≌△DMF即可解决问题;
(2)利用(1)中结论即可解决问题;
(3)延长BD交AC于P,CD于Q,令KP=QM,交AC于P,连接DK.通过证明△BDQ≌△CDP,△MDQ≌△PDK,△MDN≌△KDN证得△AMN的周长=![]() (AB+AC)=3.
(AB+AC)=3.
试题解析:(1)延长AB至F,使BF=CN,连接DF,
∵△BDC是等腰三角形,且∠BDC=120°
∴∠BCD=∠DBC=30°
∵△ABC是边长为3的等边三角形
∴∠ABC=∠BAC=∠BCA=60°
∴∠DBA=∠DCA=90°
在Rt△BDF和Rt△CND中,
∵BF=CN,DB=DC
∴△BDF≌△CND
∴∠BDF=∠CDN,DF=DN
∵∠MDN=60°
∴∠BDM+∠CDN=60°
∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边
∴△DMN≌△DMF,
∴MN=MF,
∵MF=BM+BF=MN+CN,
∴MN=BM+CN.
(2)∵MN=BM+CN,
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.
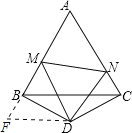
(3)延长BD交AC于P,CD于Q,令KP=QM,交AC于P,连接DK.
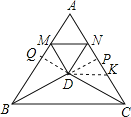
∵△BDC是等腰三角形,且∠BDC=120°
∴BD=CD,∠DBC=∠DCB=30°,∠BDQ=∠CDP=60°
又∵△ABC等边三角形
∴∠ABC=∠ACB=60°
∴∠MBD=∠PCD=30°,CQ⊥AB,BP⊥AC,
∴AQ=BQ=![]() AB=
AB=![]() ,AP=PC=
,AP=PC=![]() AC=
AC=![]() ,
,
在△BDQ和△CDP中,
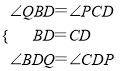 ,
,
∴△BDQ≌△CDP(ASA),
∴BQ=PC,QD=PD,
∵CQ⊥AB,BP⊥AC,
∴∠MQD=∠DPK=90°,
在△MDQ与△PDK中,
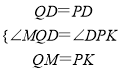 ,
,
∴△MDQ≌△PDK(SAS),
∴∠QDM=∠PDK,DM=DK,
∵∠BDQ=60°∠MDN=60°,
∴∠QDM+∠PDN=60°,
∴∠PDK+∠PDN=60°,
即∠KDN=60°,
在△MDN与△KDN中,
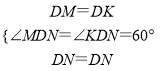 ,
,
∴△MDN≌△KDN(SAS),
∴MN=KN=NP+PK,
∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AQ+AP=![]() +
+![]() =3
=3
故△AMN的周长为3.

 名校课堂系列答案
名校课堂系列答案