Question

【题目】问题发现：

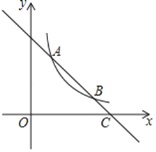
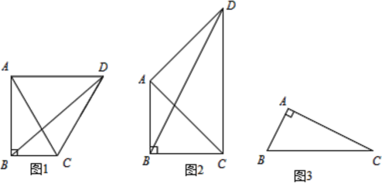
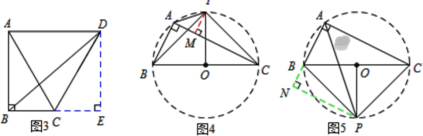
（1）如图1，在Rt△ABC中，∠BAC=30°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC， ∠BCD的度数是　　；线段BD，AC之间的数量关系是　　．

类比探究：

（2）在Rt△ABC中，∠BAC=45°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC，请问（1）中的结论还成立吗？；

拓展延伸：

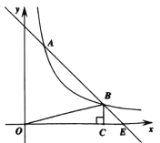
（3）如图3，在Rt△ABC中，AB＝2，AC＝4，∠BDC＝90°，若点P满足PB＝PC，∠BPC＝90°，请直接写出线段AP的长度．

Answer 1

【答案】（1）120°，BD=AC；（2）不成立，理由详见解析；（3）或．

【解析】

（1）过点D作DE⊥BC，通过线段之间的转换得到AC与DE之间的关系，在直角三角形BDE中通过BD与DE的关系，得到BD,AC之间的关系.

（2）类比（1）的解法，找线段之间的关系.

(3)分情况进行讨论，画出符合题意得图形进行求解.

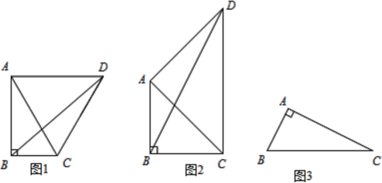
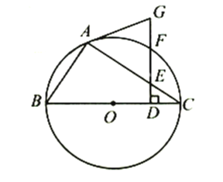
解：（1）如图3，过点D作DE⊥BC，垂足为E，设BC=m．

在Rt△ABC中，∠BAC=30°，由BC=AB·tan30°，BC=AC·sin30°，得AC=2m，BC=m，

∵AC=AD，∠CAD=2×30°=60°，∴△ACD为等边三角形，∴∠ACD=60°，CD=AC=2m，

∴∠BCD=60°×2=120°，在Rt△DEC中，∠DCE=180°-120°=60°，DC=2m，∴CE=CD·cos60°=m，DE=CE·tan60°=m，∴在Rt△BED中，BD==，

∴==，故BD=AC．故答案为：120°；BD=AC．

（2）不成立，理由如下：

设BC=n，在Rt△ABC中，∠BAC=45°，∠ABC=90°，∴BC=AB=m，AC=BC=n，

∵AC=AD，∠CAD=90°，∴△CAD为等腰直角三角形，∴∠ACD=45°，CD=AC= 2n，

∴∠BCD=2×45°=90°，在Rt△BCD中，BD==，

∴==，，故BD=AC．答案为：90°；BD=AC．故结论不成立．

（3）AP的长为或．；解答如下：

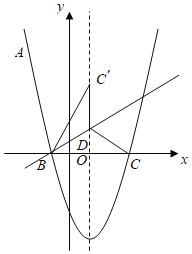
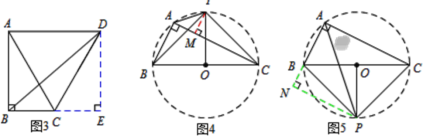
∵PB=PC，∴点P在线段BC的垂直平分线上，∵∠BAC=∠BCP=90°，故A、B、C、P四点共圆，以线段BC的中点为圆心构造⊙O，如图4，图5，分类讨论如下：

①当点P在直线BC上方时，如图4，作PM⊥AC，垂足为M，设PM=x．

∵PB=PC，∠BPC=90°，∴△PBC为等腰直角三角形，∴∠PBC=45°，

∵∠PAC=∠PBC=45°，∴△AMP为等腰直角三角形，∴AM=PM=x，AP=PM=x，

在Rt△ABC中，AB=2，AC=4，∴BC==，∴PC=BC·sin45°=，

在Rt△PMC中，∵∠PMC=90°，PM=x，PC=，CM=4-x，∴，

解得：，（舍），∴AP==；

②当点P在直线BC的下方时，如图5，作PN⊥AB的延长线，垂足为N，设PN=y．

同上可得PB=，△PAN为等腰三角形，∴AN=PN=y，∴BN=y-2，

在Rt△PNB中，∵∠PNB=90°，PN=y，BN=y-2，PB=，∴，

解得：，（舍），∴AP==．故AP的长度为：或．