题目内容
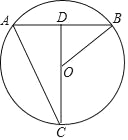
【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(2,0),∠ABO=30°,且AB⊥BC.

(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
【答案】(1)y=![]() ;(2)(﹣2,0)或(0,0)
;(2)(﹣2,0)或(0,0)
【解析】
(1)解直角三角形求出B、C两点坐标,利用待定系数法即可解决问题;
(2)如图1中,根据对称性可知,当点F与O重合时,∠EF′D=∠EBD=90°,此时F′(0,0);设DE交OB于K,作FH⊥DE于H.当△EFD≌△DF′E时,∠EFD=∠DF′E=90°,想办法求出OF的长即可解决问题;
解:(1)在Rt△AOB中,∵OA=2,∠ABO=30°,
∴OB=2![]() ,
,
在Rt△OBC中,∵∠BCO=30°,OB=2![]() ,
,
∴OC=6,
∴B(0,2![]() ),C(6,0),
),C(6,0),
设直线AB的解析式为y=kx+b,则有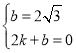 ,
,
解得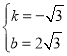 ,
,
∴直线AB的解析式为y=﹣![]() x+2
x+2![]() ,
,
设直线BC的解析式为y=k′x+b′则有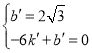 ,
,
解得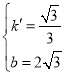 ,
,
∴直线BC的解析式为y=![]() x+2
x+2![]() .
.
(2)如图1中,根据对称性可知,当点F与O重合时,∠EF′D=∠EBD=90°,此时F′(0,0),

设DE交OB于K,作FH⊥DE于H.当△EFD≌△DF′E时,∠EFD=∠DF′E=90°,
易证DK=EH=1,DE=![]() AC=4,
AC=4,
∴KH=OF=4﹣2=2,
∴F(﹣2,0),
综上所述,满足条件的点F坐标为(﹣2,0)或(0,0).

练习册系列答案
相关题目