题目内容
如图,△ABC中,AB=AC,D是BC上一点,且BD=BA.连接AD,若∠ADB=α,∠CAD=β,则α,β满足的关系是( )
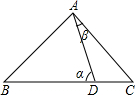
| A.α+β=90° | B.2α+β=180° | C.3α-β=180° | D.α+3β=180° |

∵BD=BA,
∴∠BAD=α,
∴△ABC中,β+∠C+∠BAD+∠B=180°,
∵AB=AC,
∴∠B=∠C,
∵α=β+∠C,
∴β+α-β+α-β+α=180°,
∴3α-β=180°.
故选C.
∴∠BAD=α,
∴△ABC中,β+∠C+∠BAD+∠B=180°,
∵AB=AC,
∴∠B=∠C,
∵α=β+∠C,
∴β+α-β+α-β+α=180°,
∴3α-β=180°.
故选C.

练习册系列答案
相关题目