题目内容
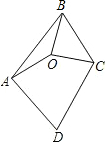
如图，已知O是四边形ABCD内一点，OA=OB=OC，∠ABC=∠ADC=70°，则∠DAO+∠DCO的大小是（ ）
| A．70° | B．110° | C．140° | D．150° |
根据四边形的内角和定理可得：
∠DAB+∠DCB=220°，
∵OA=OB=OC，∠ABC=∠ADC=70°，
∴∠OAB=∠OBA，∠OCB=∠OBC，
∴∠OAB+∠OCB=70°，
∴∠DAO+∠DCO=220°-70°=150度．
故选D．
∠DAB+∠DCB=220°，
∵OA=OB=OC，∠ABC=∠ADC=70°，
∴∠OAB=∠OBA，∠OCB=∠OBC，
∴∠OAB+∠OCB=70°，
∴∠DAO+∠DCO=220°-70°=150度．
故选D．
练习册系列答案
名校课堂系列答案
相关题目
