题目内容
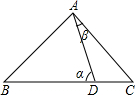
(1)如图所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F,试判断△AEF的形状,并说明理由;
(2)如图所示,已知∠BAC=90°,AD⊥BC,垂足为D,AE=AF,试说明BE平分∠ABC.
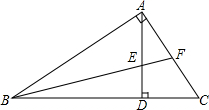
(2)如图所示,已知∠BAC=90°,AD⊥BC,垂足为D,AE=AF,试说明BE平分∠ABC.

(1)△AEF是等腰三角形,
理由如下:
∵BF平分∠ABC,
∴∠ABF=∠DBF,
又∵∠BAC=90°,AD⊥BC,
∴∠AFE=90°-∠ABF,∠DEB=90°-∠DBF,
∴∠AFE=∠DEB,
又∵∠DEB=∠AEF,
∴∠AEF=∠AFE,
∴△AEF是等腰三角形;
(2)证明:
∵∠BAC=90°,AD⊥BC,
∴∠AFE+∠ABF=90°,∠DEB+∠BED=90°,
∵AE=AF,
∴∠AFE=∠AEF,
∴∠ABF=∠DBF,
∴BF平分∠ABC.
理由如下:
∵BF平分∠ABC,

∴∠ABF=∠DBF,
又∵∠BAC=90°,AD⊥BC,
∴∠AFE=90°-∠ABF,∠DEB=90°-∠DBF,
∴∠AFE=∠DEB,
又∵∠DEB=∠AEF,
∴∠AEF=∠AFE,
∴△AEF是等腰三角形;
(2)证明:
∵∠BAC=90°,AD⊥BC,
∴∠AFE+∠ABF=90°,∠DEB+∠BED=90°,
∵AE=AF,
∴∠AFE=∠AEF,
∴∠ABF=∠DBF,
∴BF平分∠ABC.

练习册系列答案
相关题目