جâؤ؟ؤعبف
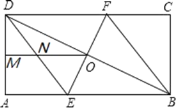
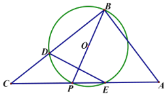
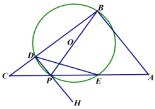
،¾جâؤ؟،؟بçح¼£¬زرضھدك¶خAB£½12cm£¬Cتادك¶خABةدز»¶¨µم£¬ازAC£½3cm£¬µمDتادك¶خBCةدµؤز»¸ِ¶¯µم£¬ةèCD£½xcm£¬زشCخھضذذؤث³ت±صëذ×ھدك¶خACزشDخھضذذؤ£¬ؤوت±صëذ×ھدك¶خDB£¬ت¹A،¢Bء½µمؤـضط؛دسعµمE£®
£¨1£©µ±C،¢D،¢Eبµمؤـ¹¹³ةب½اذخت±£¬اَxµؤب،ضµ·¶خ§£»
£¨2£©µ±xخھ؛خضµت±£¬،÷CDEتاض±½اب½اذخ£؟
£¨3£©¼ا،÷CDEµؤأو»خھScm2£¬تشاَ³ِSسëxµؤ؛¯ت±ي´ïت½£»بô،÷CDEµؤأو»خھ![]() cm2£¬تشب·¶¨´ثت±µمDµؤخ»ضأ£؟
cm2£¬تشب·¶¨´ثت±µمDµؤخ»ضأ£؟
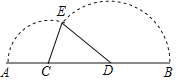
،¾´ً°¸،؟£¨1£©3£¼x£¼6£»£¨2£©µ±x£½4»ٍ5ت±£¬،÷CDEتاض±½اب½اذخ£»£¨3£©S£½![]() £»µ±S£½
£»µ±S£½![]() ت±£¬DسëµمCµؤ¾àہëخھ
ت±£¬DسëµمCµؤ¾àہëخھ![]() cm»ٍ
cm»ٍ![]() cm£®
cm£®
،¾½âخِ،؟
£¨1£©سةAC£½CE£½3£¬AB£½12£¬CD£½xضھDE£½BD£½9©پx£¬ہûسأب½اذخب±ك¹طدµ؟ةµأ´ً°¸£»
£¨2£©·ض،دDCE£½90،م£¬،دCDE£½90،م؛ح،دCED£½90،مبضضاé؟ِ£¬ہûسأ¹´¹ة¶¨ہيءذ³ِ·½³ج£¬½âض®؟ةµأ£»
£¨3£©×÷EF،حAB£¬ةèCF£½m£¬،÷CDEµؤأو»خھS£¬¸ù¾فEF2£½9©پm2£½£¨9©پx£©2©پ£¨x©پm£©2µأm£½![]() £¬سةS£½
£¬سةS£½![]() CDEFضھS2£½
CDEFضھS2£½![]() CD2EF2½«دà¹طت¾ف´ْب룬صûہي؟ةµأ؛¯ت½âخِت½£¬شظ¸ù¾فجâزâءذ³ِ·½³ج½âض®؟ةµأ£®
CD2EF2½«دà¹طت¾ف´ْب룬صûہي؟ةµأ؛¯ت½âخِت½£¬شظ¸ù¾فجâزâءذ³ِ·½³ج½âض®؟ةµأ£®
½â£؛£¨1£©،كAC£½CE£½3£¬AB£½12£¬CD£½x£¬
،àDE£½BD£½9©پx£¬
سةCD+CE£¾DEازCD©پCE£¼DE
؟ةµأ![]() £¬
£¬
½âµأ£؛3£¼x£¼6£»
£¨2£©¢ظµ±،دDCE£½90،مت±£¬
¸ù¾ف¹´¹ة¶¨ہيCD2+CE2£½DE2£¬¼´x2+32£½£¨9©پx£©2£¬
½âµأ£؛x£½4£»
¢عµ±،دCDE£½90،مت±£¬
¸ù¾ف¹´¹ة¶¨ہيCD2+DE2£½CE2£¬¼´x2+£¨9©پx£©2£½32£¬
صûہي£¬µأ£؛x2©پ9x+36£½0£¬
سة،÷£½£¨©پ9£©2©پ4،ء1،ء36£½©پ63£¼0ضھ·½³جخق½â£»
¢غµ±،دCED£½90،مت±£¬
¸ù¾ف¹´¹ة¶¨ہيCE2+DE2£½CD2£¬¼´32+£¨9©پx£©2£½x2£¬
½âµأ£؛x£½5£»
×غةد£¬µ±x£½4»ٍ5ت±£¬،÷CDEتاض±½اب½اذخ£»
£¨3£©¹µمE×÷EF،حABسعµمF£¬
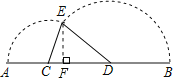
ةèCF£½m£¬،÷CDEµؤأو»خھS£¬
شٍ£؛EF2£½9©پm2£½£¨9©پx£©2©پ£¨x©پm£©2£¬
،àm£½![]() £¬
£¬
،كS£½![]() CDEF£¬
CDEF£¬
S2£½![]() CD2EF2
CD2EF2
£½![]() x2[9©پ
x2[9©پ![]() ]
]
£½©پ18£¨x2©پ9x+18£©£¬
،àS£½![]() £¬
£¬
µ±S£½![]() £½
£½![]() ت±£¬
ت±£¬
½âµأ£؛x1£½![]() £¬x2£½
£¬x2£½![]() £¬
£¬
´ثت±µمDسëµمCµؤ¾àہëخھ![]() cm»ٍ
cm»ٍ![]() cm£®
cm£®