题目内容
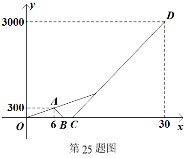
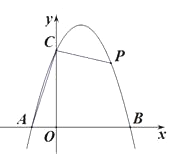
【题目】如图,抛物线 ![]() 与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
(1)抛物线的解析式为________;
(2)P为抛物线上一点,连结AC,PC,若∠PCO=3∠ACO,点P的坐标为________.
【答案】y=x2+2x+3 (![]() ,
,![]() )
)
【解析】
(1)将A、B两点坐标代入抛物线解析式得一个二元一次方程组,解之即可得出b、c值,从而可得抛物线解析式.
(2)延长CP交x轴于点E,在x轴上取点D,使CD=CA,作EN⊥CD交CD的延长线于点N,作AI⊥CD交CD于I,由等腰三角形三线合一的性质可知
∠DCO=∠ACO,结合已知条件可知∠ACD=∠ECD,由此得tan∠ACD=tan∠ECD,即![]() , 根据等面积法求得AI=
, 根据等面积法求得AI=![]() , 由勾股定理得CI=
, 由勾股定理得CI=![]() , 即
, 即![]() , 由此设EN=3x,则CN=4x,根据tan∠CDO=tan∠EDN得DN=x,由CD=CN-DN求得x值以及E点坐标,再由待定系数法求得直线CE解析式y=-
, 由此设EN=3x,则CN=4x,根据tan∠CDO=tan∠EDN得DN=x,由CD=CN-DN求得x值以及E点坐标,再由待定系数法求得直线CE解析式y=-![]() x+3,将直线CE和抛物线解析式联立、解之即可求得P点坐标.
x+3,将直线CE和抛物线解析式联立、解之即可求得P点坐标.
(1)解:∵A(-1,0),B(3,0)在抛物线上,
∴![]() ,
,
解得:![]()
∴抛物线解析式为:y=x2+2x+3.
故答案为:y=x2+2x+3.(2)延长CP交x轴于点E,在x轴上取点D,使CD=CA,作EN⊥CD交CD的延长线于点N,作AI⊥CD交CD于I,
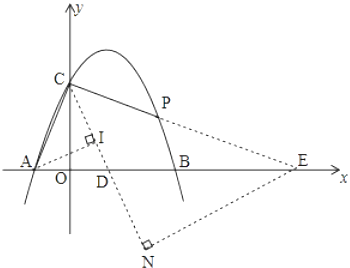
∵CD=CA,OC⊥AD,
∴∠DCO=∠ACO,
∵∠PCO=3∠ACO,
∴∠ACD=∠ECD,
∴tan∠ACD=tan∠ECD,
∴![]() ,
,
在Rt△ACI中,
又∵A(-1,0),C(0,3),
∴OA==OD=1,OC=3,
∴AD=2,AC=DC=![]()
AI=![]() ,
,
∴CI=![]() ,
,
∴![]() ,
,
设EN=3x,则CN=4x,DE=5x,
∵tan∠CDO=tan∠EDN,
∴![]() ,
,
∴DN=x,
∴CD=CN-DN=4x-x=3x=![]() ,
,
∴x=![]() ,
,
即DN=![]() , EN=
, EN=![]() ,
,
∴DE=![]() ,
, ![]()
∴E(![]() , 0),
, 0),
设直线CE解析式为:y=kx+b,
∴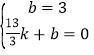 ,
,
解得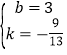 ,
,
∴直线CE解析式为:y=-![]() x+3,
x+3,
∴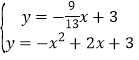 ,
,
解得:![]() (舍去)或
(舍去)或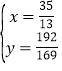 ,
,
∴P(![]() ,
,![]() ).
).

【题目】为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计如下,而且制成了如图所示的不完整的统计图.
体育成绩统计表
分数段 | 频数 | 频率 |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
体育成绩统计图

根据上面提供的信息,解答下列问题:
(1)在统计表中,a=________,b=________,并将统计图补充完整;
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗?__________(填“正确”或“错误”).
(3)若成绩在27分以上(含27分)定为优秀,则该市今年48 000名九年级学生中体育成绩为优秀的学生约有多少?