题目内容
【题目】在一副三角板ABC和DEC中,∠ACB=∠CDE=90°,∠BAC=60°,∠DEC=45°. 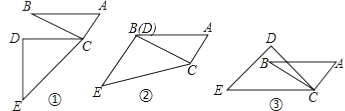
(1)当AB∥DC时,如图①,求∠DCB的度数.
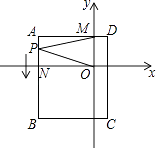
(2)当CD与CB重合时,如图②,判断DE与AC的位置关系,并说明理由.
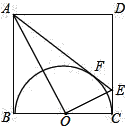
(3)如图③,当∠DCB等于多少度时,AB∥EC?
【答案】
(1)解:∵∠BCA=90°,∠A=60°,
∴∠B=180°﹣90°﹣60°=30°,
∵AB∥CD,
∴∠DCB=∠B=30°
(2)解:DE∥AC,
理由是:∵∠EDC=90°,∠DEC=45°,
∴∠DCE=45°,
∵∠BCA=90°,
∴∠ACE+∠DEC=90°+45°+45°=180°,
∴DE∥AC
(3)解:当∠DCB等于15度时,AB∥EC,
理由是:∵∠DCB=15°,∠DCE=45°,
∴∠BCE=45°﹣15°=30°,
∴∠B=30°,
∴∠B=∠BCE,
∴AB∥EC,
即当∠DCB等于15度时,AB∥EC
【解析】(1)求出∠B,根据平行线的判定推出即可;(2)求出∠ACE+∠E=180°,根据平行线的判定推出即可;(3)求出∠BCE=∠B,根据平行线的判定推出即可.
【考点精析】通过灵活运用平行线的判定与性质,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质即可以解答此题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目