题目内容
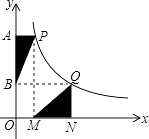
【题目】如图，在直角坐标系中，第一次将△OAB交换成△OA1B1 ， 第二次将△OA1B1变换成△OA2B2 ， 第三次将△OA2B2变换成△OA3B3…已知A（1，3），A1（2，3），A2（4，3），A3（8，3），B（2，0），B1（4，0），B2（8，0），B3（16，0）．观察每次变换前后的三角形有何变化，按照变换规律，第五次变换后得到的三角形A5的坐标是 ， B5的坐标是 ， An的坐标是 ．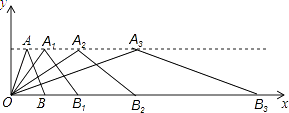 
【答案】（32，3）；（64，0）；（2n ， 3）
【解析】解：∵A（1，3），A1（2，3），A2（4，3），A3（8，3）…，
∴纵坐标不变为3，横坐标都和2有关，为2n ，
∴A5（32，3）；
∵B（2，0），B1（4，0），B2（8，0），B3（16，0）…
∴纵坐标不变，为0，横坐标都和2有关为2n+1 ，
∴B5的坐标为（64，0）；
由上题规律可知An的纵坐标总为3，横坐标为2n ， 即（2n ， 3），
所以答案是：（32，3）|（64，0）|（2n ， 3）．
【考点精析】掌握数与式的规律是解答本题的根本，需要知道先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
