��Ŀ����
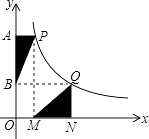
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ABCDΪ�����Σ����е�A��C����ֱ�Ϊ����4��2������1����4������AD��x�ᣬ��y����M�㣬AB��x����N��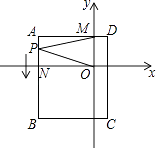
��1����B��D��������ͳ�����ABCD�������
��2��һ����P��A�������� ![]() ����λ/����ٶ���AB��B���˶�����P���˶������У�����MP��OP����ֱ��д����AMP����MPO����PON֮���������ϵ��
����λ/����ٶ���AB��B���˶�����P���˶������У�����MP��OP����ֱ��д����AMP����MPO����PON֮���������ϵ��
��3���Ƿ����ijһʱ��t��ʹ������AMP��������ڳ���������� ![]() �������ڣ���t��ֵ�����ʱ��P�����ꣻ��������˵�����ɣ�
�������ڣ���t��ֵ�����ʱ��P�����ꣻ��������˵�����ɣ�
���𰸡�
��1��
�⣺�ߵ�A��C����ֱ�Ϊ����4��2������1����4����
���ı���ABCDΪ���Σ�
��B����4����4����D��1��2����
����ABCD�����=��1+4������2+4��=30
��2��
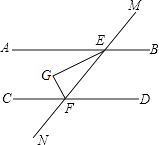
�⣺����P���߶�AN��ʱ����PQ��AM����ͼ��
��AM��ON��
��AM��PQ��ON��
���QPM=��AMP����QPO=��PON��
���QPM+��QPO=��AMP+��PON��
����MPO=��AMP+��PON��
����P���߶�NB��ʱ��ͬ�������ɵá�MPO=��AMP����PON
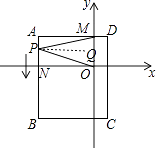
��3��
�⣺���ڣ�
��AM=4��AP= ![]() t��
t��
��S��AMP= ![]() ��4��
��4�� ![]() t=t��
t=t��
��������AMP��������ڳ���������� ![]() ��
��
��t=30�� ![]() =10��
=10��
��AP= ![]() ��10=5��
��10=5��
��AN=2��
��P����������4����3����
����������1�����õ�A��C������;��ε�������B����4����4����D��1��2����Ȼ����ݾ��������ʽ�������ABCD���������2���������ۣ�����P���߶�AN��ʱ����PQ��AM����ͼ������ƽ���ߵ������á�QPM=��AMP����QPO=��PON�����MPO=��AMP+��PON������P���߶�NB��ʱ��ͬ�������ɵá�MPO=��AMP����PON����3������AM=4��AP= ![]() t�����������������ʽ�õ�S��AMP=t��������������AMP��������ڳ����������
t�����������������ʽ�õ�S��AMP=t��������������AMP��������ڳ���������� ![]() �ɼ����t=10����AP=5��Ȼ����ݵ������ı�ʾ����д��P�����꣮
�ɼ����t=10����AP=5��Ȼ����ݵ������ı�ʾ����д��P�����꣮
�����㾫����������Ŀ����֪���������������ε���������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ε����=1/2���ס��ߣ�

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�