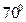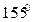题目内容
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整。
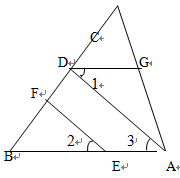
解:∵EF∥AD ( 已知 )
∴∠2=_______( )
又∵∠1=∠2 ( 已知 )
∴∠1=∠3
∴AB∥_______( )
∴∠BAC+_____=180°
又∵∠BAC=70°
∴∠AGD=_______

解:∵EF∥AD ( 已知 )
∴∠2=_______( )
又∵∠1=∠2 ( 已知 )
∴∠1=∠3
∴AB∥_______( )
∴∠BAC+_____=180°
又∵∠BAC=70°
∴∠AGD=_______

根据题意,利用平行线的性质和判定填空即可.
解:∵EF∥AD(已知),
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠DGA=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.
主要考查了平行四边形的性质和判定定理等知识点,理解平行四边形的性质和判定定理进行证明是解此题的关键.
解:∵EF∥AD(已知),
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠DGA=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.
主要考查了平行四边形的性质和判定定理等知识点,理解平行四边形的性质和判定定理进行证明是解此题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
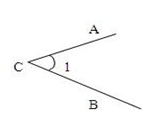



 ABD
ABD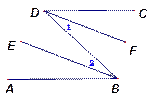
 ∠2=
∠2= ,
,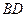 平分
平分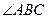 ,若
,若 ,则
,则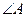 的度数是
的度数是