题目内容
【题目】如图所示,已知四边形ABCD、ADEF都是菱形,∠BAD=∠FAD, ∠BAD为锐角.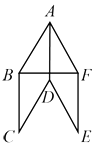
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数。
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB=AD,
又∵四边形ADEF是菱形,
∴AF=AD,
∴AB=AF,
∵∠BAD=∠FAD,
∴AD⊥BF.
(2)解:∵四边形ABCD、ADEF都是菱形,
∴AB=BC=AF,
∵BF=BC,
∴AB=AF= BF,
∴△ABF是等边三角形,
∴∠BAF=60°,
∵∠BAD=∠FAD,
∴∠BAD=30°,
∵四边形ABCD是菱形,
∴AB//CD,
∴∠BAD+∠ADC=180°,
∴∠ADC=150°.
【解析】(1)由菱形的性质得AB=AD,AF=AD,等量代换得AB=AF,又∠BAD=∠FAD,根据等腰三角形三线合一的性质得AD⊥BF.
(2)由菱形的性质得AB=BC=AF,又BF=BC,等量代换得AB=AF= BF,由等边三角形的判定知△ABF是等边三角形,根据等边三角形和菱形的性质得
∠BAD=30°,由菱形和平行线的性质得∠ADC=150°.
【考点精析】利用等腰三角形的性质和菱形的性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
相关题目