题目内容
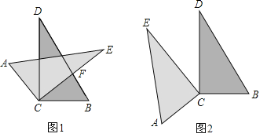
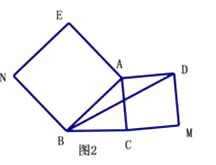
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: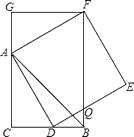
①AC=FG; ②S△FAB:S四边形CBFG=1:2;
③∠ABC=∠ABF; ④AD2=FQAC,
其中正确的结论的个数是( )
A.1
B.2
C.3
D.4
【答案】D
【解析】①∵四边形ADEF为正方形,
∴AD=AF,∠FAD=90°,
∴∠FAG+∠CAD=90°,
又∵FG⊥CA,
∴∠FGA=90°,
∴∠FAG+∠AFG=90°,
∴∠CAD=∠AFG,
在△AGF和△DCA中,
∵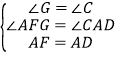 ,
,
∴△AGF≌△DCA(AAS),
∴FG=CA.
故①正确.
②∵BC=AC,FG=CA,
∴BC=FG,
又∵FG⊥CA,∠ACB=90°,
∴FG∥BC,
∴四边形BCGF是平行四边形,
又∵∠ACB=90°,
∴平行四边形BCGF是矩形,
∴∠CBF=90°,
∴S△FAB=![]() BFBC,
BFBC,
S四边形CBFG=BFBC,
∴S△FAB:S四边形CBFG=1:2;
故②正确.
③∵CA=CB,∠C=∠CBF=90°,
∴∠BAC=∠CBA=45°,
∴∠FBA=45°,
故③正确.
④∵∠ADE=∠CBF=90°,
∴∠ADC+∠BDQ=90°,
∠BQD+∠BDQ=90°,
∴∠ADC=∠BQD,
又∵∠FQE=∠BQD,
∴∠ADC=∠FQE,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:FE=AD:FQ,
又∵FE=AD,
∴AD2=FQAC,
故④正确.
所以答案是:D.
【考点精析】利用正方形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 阅读快车系列答案
阅读快车系列答案