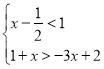题目内容
【题目】已知1辆甲型客车和1辆乙型客车共可载客75人．已知1辆甲型客车和2辆乙型客车共可载客105人．某学校计划租用两种型号客车送234名学生和6名老师集体外出活动．从安全角度考虑每辆车上至少要有1名老师，并且总费用不超过2280元．
（1）求每辆甲型客车和每辆乙型客车分别可载多少人？
（2）共需租辆客车？
（3）若每辆甲型客车和每辆乙型客车的租金分别为400元和280元，设租甲型客车x辆，总费用为W元，请你给出最节省的租车方案．
【答案】
（1）解：设每辆甲型客车可载a人，每辆乙型客车可载b人，
根据题意得： 
，
解得： 
．
答：每辆甲型客车可载45人，每辆乙型客车可载30人．
（2）6
（3）解：设租甲型客车x辆，总费用为W元，则租乙型客车（6﹣x）辆，
根据题意得：W=400x+280（6﹣x）=120x+1680．
∵共有师生234+6=240（人），
∴45x+30（6﹣x）≥240，
解得：x≥4．
∵在W=120x+1680中，k=120＞0，
∴W值随x值增大而增大，
∴当x=4时，W取最小值，最小值为2160．
答：当租甲型客车4辆、乙型客车2辆时，租车费用最少，最少费用为2160元．
【解析】解：（1）设每辆甲型客车可载a人，每辆乙型客车可载b人，
根据题意得： ，
解得： ．
答：每辆甲型客车可载45人，每辆乙型客车可载30人．
（2）∵（234+6）÷45=5 
（辆），且只有6名老师，
∴共需租6辆客车．
（3）设租甲型客车x辆，总费用为W元，则租乙型客车（6﹣x）辆，
根据题意得：W=400x+280（6﹣x）=120x+1680．
∵共有师生234+6=240（人），
∴45x+30（6﹣x）≥240，
解得：x≥4．
∵在W=120x+1680中，k=120＞0，
∴W值随x值增大而增大，
∴当x=4时，W取最小值，最小值为2160．
答：当租甲型客车4辆、乙型客车2辆时，租车费用最少，最少费用为2160元．
所以答案是：（1）每辆甲型客车可载45人，每辆乙型客车可载30人；（2）6；（3）当租甲型客车4辆、乙型客车2辆时，租车费用最少，最少费用为2160元．
