题目内容
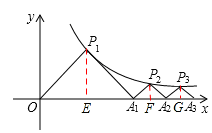
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)都在函数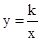 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).

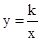 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
(1,1);( ,
,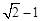 );
);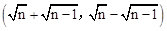 .
.
 ,
,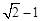 );
);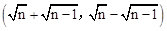 .
.试题分析:如图,过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,
∵△P1OA1是等腰直角三角形,∴P1E=OE=A1E=OA1.∴OA1=2 x1.
∵A1的坐标为(2,0),∴x1= y1=1.∴P1(1,1).
将点P1(1,1)代入
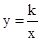 得
得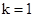 .∴反比例函数关系式为
.∴反比例函数关系式为 (x>0).
(x>0).设点P2的坐标为(b+2,b),
将点P1(b+2,b)代入
 ,可得b=
,可得b=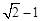 ,
,∴点P2的坐标为(
 ,
,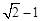 ).
).∴A1F=A2F=
 ,OA2=OA1+A1A2=
,OA2=OA1+A1A2=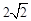 .
.设点P3的坐标为(c+
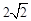 ,c),将点P3(c+
,c),将点P3(c+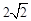 ,c)代入
,c)代入 ,可得c=
,可得c= .
.∴点P3的坐标为
 .
.综上可得:P1的坐标为(1,1),P2的坐标为(
 ,
,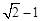 ),P3的坐标为
),P3的坐标为 ,总结规律可得:Pn坐标为:
,总结规律可得:Pn坐标为: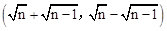 .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 在第一象限内的图像与△ABC有交点,则
在第一象限内的图像与△ABC有交点,则 的取值范围是
的取值范围是


 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到 的图象,则
的图象,则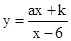 的图象经过B、E两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
的图象经过B、E两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.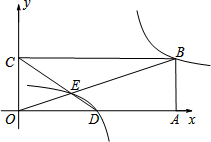
 ,AE=
,AE=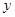 ,则能反映
,则能反映

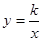 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .
的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .
 在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
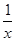 的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 .
的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 .