Question

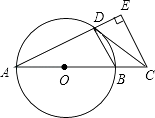
【题目】如图，将圆形纸片沿弦AB折叠后，圆弧恰好能经过圆心O，⊙O的切线BC与AO延长线交于点C．
（1）若⊙O半径为6cm，用扇形OAB围成一个圆锥的侧面，求这个圆锥的底面圆半径．
（2）求证：AB=BC．

Answer 1

【答案】
（1）

解：设圆锥的底面圆半径为r，

过O作OD⊥AB于E，交⊙O于D，连接OB，

有折叠可得 OE= OD，

∵OD=OA，

∴OE= OA，

∴在Rt△AOE中∠OAE=30°，则∠AOE=60°，

∵OD⊥AB，

∴∠AOB=2∠AOE=120°，

∴弧AB的长为： =4π，

∴2πr=4π，

∴r=2；

（2）

解：连接OB，

∵∠AOB=120°，

∴∠BOC=60°，

∵BC是⊙O的切线，

∴∠CBO=90°

∴∠C=30°，

∴∠OAE=∠C，

∴AB=BC．

；

解：连接OB，

∵∠AOB=120°，

∴∠BOC=60°，

∵BC是⊙O的切线，

∴∠CBO=90°

∴∠C=30°，

∴∠OAE=∠C，

∴AB=BC．

；解：连接OB，；

∵∠AOB=120°，

∴∠BOC=60°，

∵BC是⊙O的切线，

∴∠CBO=90°

∴∠C=30°，

∴∠OAE=∠C，

∴AB=BC．

【解析】（1）过O作OD⊥AB于E，交⊙O于D，根据题意OE= OA，得出∠OAE=30°，∠AOE=60°，从而求得∠AOB=2∠AOE=120°，根据弧长公式求得弧AB的长，然后根据圆锥的底面周长等于弧长得出2πr=4π，即可求得这个圆锥的底面圆半径；（2）连接OB，根据切线的性质得出∠OBC=90°，根据三角形外角的性质得出∠C=30°，从而得出∠BAC=∠C，根据等角对等边即可证得结论．
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径，以及对圆锥的相关计算的理解，了解圆锥侧面展开图是一个扇形，这个扇形的半径称为圆锥的母线；圆锥侧面积S=πrl；V圆锥=1/3πR2h.．